Whitehead torsion
In geometric topology, the obstruction to a homotopy equivalence 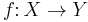 of finite CW-complexes being a simple homotopy equivalence is its Whitehead torsion
of finite CW-complexes being a simple homotopy equivalence is its Whitehead torsion 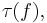 which is an element in the Whitehead group
which is an element in the Whitehead group 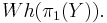 These are named after the mathematician J. H. C. Whitehead.
These are named after the mathematician J. H. C. Whitehead.
The Whitehead torsion is important in applying surgery theory to non-simply connected manifolds of dimension >4: for simply-connected manifolds, the Whitehead group vanishes, and thus homotopy equivalences and simple homotopy equivalences are the same. The applications are to differentiable manifolds, PL manifolds and topological manifolds. The proofs were first obtained in the early 1960's by Smale, for differentiable manifolds. The development of handlebody theory allowed much the same proofs in the differentiable and PL categories. The proofs are much harder in the topological category, requiring the theory of Kirby and Siebenmann. The restriction to manifolds of dimension >4 are due to the application of the Whitney trick for removing double points.
In generalizing the h-cobordism theorem, which is a statement about simply connected manifolds, to non-simply connected manifolds, one must distinguish simple homotopy equivalences and non-simple homotopy equivalences. While an h-cobordism W between simply-connected closed connected manifolds M and N of dimension n > 4 is isomorphic to a cylinder (the corresponding homotopy equivalence can be taken to be a diffeomorphism, PL-isomorphism, or homeomorphism, respectively), the s-cobordism theorem states that if the manifolds are not simply-connected, an h-cobordism is a cylinder if and only if the Whitehead torsion of the inclusion 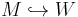 vanishes.
vanishes.
Contents |
The Whitehead group
The Whitehead group of a CW-complex or a manifold M is equal to the Whitehead group Wh(π1(M)) of the fundamental group π1(M) of M.
If G is a group, the Whitehead group Wh(G) is defined to be the cokernel of the map ![G \times \{\pm 1\} \to K_1(\mathbf{Z}[G])](/2012-wikipedia_en_all_nopic_01_2012/I/36c82ec972cf612e9618f5ade6d8763f.png) which sends (g,±1) to the invertible (1,1)-matrix (±g). Here Z[G] is the group ring of G. Recall that the K-group
which sends (g,±1) to the invertible (1,1)-matrix (±g). Here Z[G] is the group ring of G. Recall that the K-group 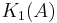 of a ring A is defined as the quotient of GL∞(A) by the subgroup generated by elementary matrices. The group GL∞(A) is the direct limit of the finite dimensional groups
of a ring A is defined as the quotient of GL∞(A) by the subgroup generated by elementary matrices. The group GL∞(A) is the direct limit of the finite dimensional groups 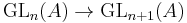 ; concretely, the group of invertible infinite matrices which differ from the identity matrix in only a finite number of coefficients. An elementary matrix here is a transvection: one such that all main diagonal elements are 1 and there is at most one non-zero element not on the diagonal. The subgroup generated by elementary matrices is exactly the derived subgroup, in other words the smallest normal subgroup such that the quotient by it is abelian.
; concretely, the group of invertible infinite matrices which differ from the identity matrix in only a finite number of coefficients. An elementary matrix here is a transvection: one such that all main diagonal elements are 1 and there is at most one non-zero element not on the diagonal. The subgroup generated by elementary matrices is exactly the derived subgroup, in other words the smallest normal subgroup such that the quotient by it is abelian.
In other words, the Whitehead group Wh(G) of a group G is the quotient of GL∞(A) by the subgroup generated by elementary matrices, elements of G and -1. Notice that this is the same as the quotient of the reduced K-group ![{\tilde K}_1(\mathbf{Z}[G])](/2012-wikipedia_en_all_nopic_01_2012/I/a0cb37fd15ebdd115209f1be27132f05.png) by G.
by G.
Examples
- The Whitehead group of the trivial group is trivial. Since the group ring of the trivial group is Z, we have to show that any matrix can be written as a product of elementary matrices times a diagonal matrix; this follows easily from the fact that Z is a Euclidean domain.
- The Whitehead group of a free abelian group is trivial, a 1964 result of Bass, Heller and Swan. This is quite hard to prove, but is important as it is used in the proof that an s-cobordism of dimension at least 6 whose ends are tori is a product. It is also the key algebraic result used in the surgery theory classification of piecewise linear manifolds of dimension at least 5 which are homotopy equivalent to a torus; this is the essential ingredient of the 1969 Kirby-Siebenmann structure theory of topological manifolds of dimension at least 5.
- The Whitehead group of a braid group (or any subgroup of a braid group) is trivial. This was proved by Farrell and Roushon.
- The Whitehead group of the cyclic groups of orders 2, 3, 4, and 6 are trivial.
- The Whitehead group of the cyclic group of order 5 is Z. This was proved in 1940 by Higman. An example of a non-trivial unit in the group ring is (1−t−t4)(1−t2−t3)=1, where t is a generator of the cyclic group of order 5. This example is closely related to the existence of units of infinite order in the ring of integers of the cyclotomic field generated by fifth roots of unity.
- The Whitehead group of any finite group G is finitely generated, of rank equal to the number of irreducible real representations of G minus the number of irreducible rational representations. this was proved in 1965 by Bass.
- If G is a finite abelian group then K1(Z[G]) is isomorphic to the units of the group ring Z[G] under the determinant map, so Wh(G) is just the group of units of Z[G] modulo the group of "trivial units" generated by elements of G and −1.
- It is a well-known conjecture that the Whitehead group of any torsion-free group should vanish.
The Whitehead torsion
At first we define the Whitehead torsion 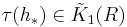 for a chain homotopy equivalence
for a chain homotopy equivalence 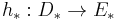 of finite based free R-chain complexes. We can assign to the homotopy equivalence its mapping cone C* := cone*(h*) which is a contractible finite based free R-chain complex. Let
of finite based free R-chain complexes. We can assign to the homotopy equivalence its mapping cone C* := cone*(h*) which is a contractible finite based free R-chain complex. Let 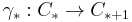 be any chain contraction of the mapping cone, i.e.
be any chain contraction of the mapping cone, i.e. 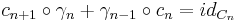 for all
for all  . We obtain an isomorphism
. We obtain an isomorphism 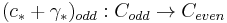 with
with  ,
,  . We define
. We define ![\tau(h_*)�:= [A] \in {\tilde K}_1(R)](/2012-wikipedia_en_all_nopic_01_2012/I/b7fb4765a4e6e92aa555c839f4f5d053.png) , where A is the matrix of (c* + γ*)odd with respect to the given bases.
, where A is the matrix of (c* + γ*)odd with respect to the given bases.
For a homotopy equivalence 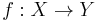 of connected finite CW-complexes we define the Whitehead torsion
of connected finite CW-complexes we define the Whitehead torsion 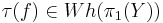 as follows. Let
as follows. Let 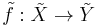 be the lift of
be the lift of 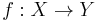 to the universal covering. It induces Z[π1(Y)]-chain homotopy equivalences
to the universal covering. It induces Z[π1(Y)]-chain homotopy equivalences 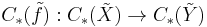 . Now we can apply the definition of the Whitehead torsion for a chain homotopy equivalence and obtain an element in
. Now we can apply the definition of the Whitehead torsion for a chain homotopy equivalence and obtain an element in ![{\tilde K}_1(\mathbf{Z}[\pi_1(Y)])](/2012-wikipedia_en_all_nopic_01_2012/I/274124de6838555f805097778c1aaa7f.png) which we map to
which we map to 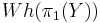 . This is the Whitehead torsion
. This is the Whitehead torsion 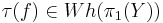 .
.
Properties
Homotopy invariance: Let 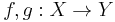 be homotopy equivalences of finite connected CW-complexes. If
be homotopy equivalences of finite connected CW-complexes. If  and
and  are homotopic then
are homotopic then  .
.
Topological invariance: If 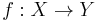 is a homeomorphism of finite connected CW-complexes then
is a homeomorphism of finite connected CW-complexes then 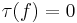 .
.
Composition formula: Let 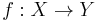 ,
, 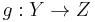 be homotopy equivalences of finite connected CW-complexes. Then
be homotopy equivalences of finite connected CW-complexes. Then 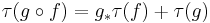 .
.
Geometric interpretation
The s-cobordism theorem states for a closed connected oriented manifold M of dimension  > 4 that an h-cobordism W between M and another manifold N is trivial over M if and only if the Whitehead torsion of the inclusion
> 4 that an h-cobordism W between M and another manifold N is trivial over M if and only if the Whitehead torsion of the inclusion 
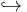
 vanishes. Moreover, for any element in the Whitehead group there exists an h-cobordism
vanishes. Moreover, for any element in the Whitehead group there exists an h-cobordism  over
over  whose Whitehead torsion is the considered element. The proofs use handlebody decompositions.
whose Whitehead torsion is the considered element. The proofs use handlebody decompositions.
There exists a homotopy theoretic analogue of the s-cobordism theorem. Given a CW-complex A, consider the set of all pairs of CW-complexes (X,A) such that the inclusion of A into X is a homotopy equivalence. Two pairs (X1,A) and (X2,A) are said to be equivalent, if there is a simple homotopy equivalence between X1 and X2 relative to A. The set of such equivalence classes form a group where the addition is given by taking union of X1 and X2 with common subspace A. This group is natural isomorphic to the Whitehead group Wh(A) of the CW-complex A. The proof of this fact is similar to the proof of s-cobordism theorem.
See also
References
- Bass, H., Heller, A. and Swan, R. The Whitehead group of a polynomial extension, Inst. Hautes \'Etudes Sci. Publ. Math. 22 1964 61--79
- Cohen, M. A course in simple homotopy theory Graduate Text in Mathematics 10, Springer, 1973
- Higman, G. The units of group-rings Proc. London Math. Soc. (2) 46 1940 231--248
- Kirby, R. and Siebenmann, L. Foundational essays on topological manifolds, smoothings, and triangulations. Annals of Mathematics Studies, No. 88. Princeton University Press, Princeton, N.J.; University of Tokyo Press, Tokyo, 1977.
- Milnor, J. Whitehead torsion Bull. Amer. Math. Soc. 72 1966 358--426.
- Smale, S. On the structure of manifolds. Amer. J. Math. 84 1962 387--399.
- Whitehead, J.H.C. Simple homotopy types Amer. J. Math. 72 1950 1--57