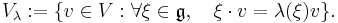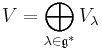Weight (representation theory)
In the mathematical field of representation theory, a weight of an algebra A over a field F is an algebra homomorphism from A to F – a linear functional – or equivalently, a one dimensional representation of A over F. It is the algebra analogue of a multiplicative character of a group. The importance of the concept, however, stems from its application to representations of Lie algebras and hence also to representations of algebraic and Lie groups. In this context, a weight of a representation is a generalization of the notion of an eigenvalue, and the corresponding eigenspace is called a weight space.
Contents |
Motivation and general concept
Weights
Given a set S of matrices, each of which is diagonalizable, and any two of which commute, it is always possible to simultaneously diagonalize all of the elements of S.[note 1][note 2] Equivalently, for any set S of mutually commuting semisimple linear transformations of a finite-dimensional vector space V there exists a basis of V consisting of simultaneous eigenvectors of all elements of S. Each of these common eigenvectors v ∈ V, defines a linear functional on the subalgebra U of End(V) generated by the set of endomorphisms S; this functional is defined as the map which associates to each element of U its eigenvalue on the eigenvector v. This "generalized eigenvalue" is a prototype for the notion of a weight.
The notion is closely related to the idea of a multiplicative character in group theory, which is a homomorphism χ from a group G to the multiplicative group of a field F. Thus χ: G → F× satisfies χ(e) = 1 (where e is the identity element of G) and
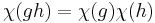 for all g, h in G.
for all g, h in G.
Indeed, if G acts on a vector space V over F, each simultaneous eigenspace for every element of G, if such exists, determines a multiplicative character on G; the eigenvalue on this common eigenspace of each element of the group.
The notion of multiplicative character can be extended to any algebra A over F, by replacing χ: G → F× by a linear map χ: A → F with
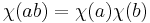 for all a, b in A.
for all a, b in A.
If an algebra A acts on a vector space V over F to any simultaneous eigenspace corresponds an algebra homomorphism from A to F assigning to each element of A its eigenvalue.
If A is a Lie algebra, then the commutativity of the field and the anticommutativity of the Lie bracket imply that this map vanish on commutators : χ([a,b])=0. A weight on a Lie algebra g over a field F is a linear map λ: g → F with λ([x,y])=0 for all x, y in g. Any weight on a Lie algebra g vanishes on the derived algebra [g,g] and hence descends to a weight on the abelian Lie algebra g/[g,g]. Thus weights are primarily of interest for abelian Lie algebras, where they reduce to the simple notion of a generalized eigenvalue for space of commuting linear transformations.
If G is a Lie group or an algebraic group, then a multiplicative character θ: G → F× induces a weight χ = dθ: g → F on its Lie algebra by differentiation. (For Lie groups, this is differentiation at the identity element of G, and the algebraic group case is an abstraction using the notion of a derivation.)
Weight space of a representation
Let V be a representation of a Lie algebra g over a field F and let λ be a weight of g. Then the weight space of V with weight λ: g → F is the subspace
A weight of the representation V is a weight λ such that the corresponding weight space is nonzero. Nonzero elements of the weight space are called weight vectors.
If V is the direct sum of its weight spaces
then it is called a weight module; this corresponds to having an eigenbasis (a basis of eigenvectors), i.e., being a diagonalizable matrix.
Similarly, we can define a weight space Vλ for any representation of a Lie group or an associative algebra.
Semisimple Lie algebras
Let g be a Lie algebra, h a maximal commutative Lie subalgebra consisting of semi-simple elements (sometimes called Cartan subalgebra) and let V be a finite dimensional representation of g. If g is semisimple, then [g,g] = g and so all weights on g are trivial. However, V is, by restriction, a representation of h, and it is well known that V is a weight module for h, i.e., equal to the direct sum of its weight spaces. By an abuse of language, the weights of V as a representation of h are often called weights of V as a representation of g.
Similar definitions apply to a Lie group G, a maximal commutative Lie subgroup H and any representation V of G. Clearly, if λ is a weight of the representation V of G, it is also a weight of V as a representation of the Lie algebra g of G.
If V is the adjoint representation of g, its weights are called roots, the weight spaces are called root spaces, and weight vectors are sometimes called root vectors.
We now assume that g is semisimple, with a chosen Cartan subalgebra h and corresponding root system. Let us suppose also that a choice of positive roots 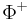 has been fixed. This is equivalent to the choice of a set of simple roots.
has been fixed. This is equivalent to the choice of a set of simple roots.
Ordering on the space of weights
Let 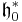 be the real subspace of
be the real subspace of 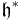 (if it is complex) generated by the roots of
(if it is complex) generated by the roots of  .
.
There are two concepts how to define an ordering of 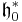 .
.
The first one is
- μ ≤ λ if and only if λ − μ is nonnegative linear combination of simple roots.
The second concept is given by an element 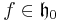 and
and
- μ ≤ λ if and only if μ(f) ≤ λ(f).
Usually, f is chosen so that β(f) > 0 for each positive root β.
Integral weight
A weight 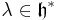 is integral (or
is integral (or  -integral), if
-integral), if 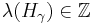 for each coroot
for each coroot 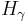 such that
such that  is a positive root.
is a positive root.
The fundamental weights  are defined by the property that they form a basis of
are defined by the property that they form a basis of 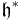 dual to the set of simple coroots
dual to the set of simple coroots  .
.
Hence λ is integral if it is an integral combination of the fundamental weights. The set of all  -integral weights is a lattice in
-integral weights is a lattice in 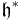 called weight lattice for
called weight lattice for  , denoted by
, denoted by 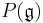 .
.
A weight λ of the Lie group G is called integral, if for each 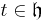 such that
such that 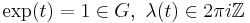 . For G semisimple, the set of all G-integral weights is a sublattice
. For G semisimple, the set of all G-integral weights is a sublattice 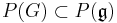 . If G is simply connected, then
. If G is simply connected, then  . If G is not simply connected, then the lattice
. If G is not simply connected, then the lattice 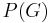 is smaller than
is smaller than 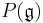 and their quotient is isomorphic to the fundamental group of G.
and their quotient is isomorphic to the fundamental group of G.
Dominant weight
A weight λ is dominant, if 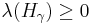 for each coroot
for each coroot 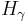 such that γ is a positive root. Equivalently, λ is dominant, if it is a non-negative linear combination of the fundamental weights.
such that γ is a positive root. Equivalently, λ is dominant, if it is a non-negative linear combination of the fundamental weights.
The convex hull of the dominant weights is sometimes called the fundamental Weyl chamber.
Sometimes, the term dominant weight is used to denote a dominant (in the above sense) and integral weight.
Highest weight
A weight λ of a representation V is called highest-weight, if no other weight of V is larger than λ. Sometimes, it is assumed that a highest weight is a weight, such that all other weights of V are strictly smaller than λ in the partial ordering given above. The term highest weight denotes often the highest weight of a "highest-weight module".
Similarly, we define the lowest weight.
The space of all possible weights is a vector space. Let's fix a total ordering of this vector space such that a nonnegative linear combination of positive vectors with at least one nonzero coefficient is another positive vector.
Then, a representation is said to have highest weight λ if λ is a weight and all its other weights are less than λ.
Similarly, it is said to have lowest weight λ if λ is a weight and all its other weights are greater than it.
A weight vector 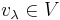 of weight λ is called a highest-weight vector, or vector of highest weight, if all other weights of V are smaller than λ.
of weight λ is called a highest-weight vector, or vector of highest weight, if all other weights of V are smaller than λ.
Highest-weight module
A representation V of  is called highest-weight module if it is generated by a weight vector
is called highest-weight module if it is generated by a weight vector 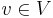 that is annihilated by the action of all positive root spaces in
that is annihilated by the action of all positive root spaces in  .
.
This is something more special than a  -module with a highest weight.
-module with a highest weight.
Similarly we can define a highest-weight module for representation of a Lie group or an associative algebra.
Verma module
For each weight 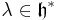 , there exists a unique (up to isomorphism) simple highest-weight
, there exists a unique (up to isomorphism) simple highest-weight  -module with highest weight λ, which is denoted L(λ).
-module with highest weight λ, which is denoted L(λ).
It can be shown that each highest weight module with highest weight λ is a quotient of the Verma module M(λ). This is just a restatement of universality property in the definition of a Verma module.
A highest-weight module is a weight module. The weight spaces in a highest-weight module are always finite dimensional.
See also
Notes
- ^ The converse is also true – a set of diagonalizable matrices commutes if and only if the set is simultaneously diagonalisable (Horn & Johnson 1985, pp. 51–53).
- ^ In fact, given a set of commuting matrices over an algebraically closed field, they are simultaneously triangularizable, without needing to assume that they are diagonalizable.
References
- Fulton, William; Harris, Joe (1991), Representation theory. A first course, Graduate Texts in Mathematics, Readings in Mathematics, 129, New York: Springer-Verlag, ISBN 978-0-387-97495-8, MR1153249, ISBN 978-0-387-97527-6.
- Goodman, Roe; Wallach, Nolan R. (1998), Representations and Invariants of the Classical Groups, Cambridge University Press, ISBN 978-0521663489.
- Humphreys, James E. (1972a), Introduction to Lie Algebras and Representation Theory, Birkhäuser, ISBN 978-0387900537.
- Horn, Roger A.; Johnson, Charles R. (1985), Matrix Analysis, Cambridge University Press, ISBN 978-0-521-38632-6
- Humphreys, James E. (1972b), Linear Algebraic Groups, Graduate Texts in Mathematics, 21, Berlin, New York: Springer-Verlag, ISBN 978-0-387-90108-4, MR0396773
- Knapp, Anthony W. (2002), Lie Groups Beyond an Introduction (2nd ed.), Birkhäuser, ISBN 978-0817642594.