Monotonicity of entailment

Monotonicity of entailment is a property of many logical systems that states that the hypotheses of any derived fact may be freely extended with additional assumptions. In sequent calculi this property can be captured by an inference rule called weakening, or sometimes thinning, and in such systems one may say that entailment is monotone if and only if the rule is admissible. Logical systems with this property are occasionally called monotonic logics in order to differentiate them from non-monotonic logics.

Weakening rule

To illustrate, starting from the natural deduction sequent:

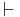Γ C

weakening allows one to conclude:

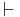Γ, A C

Non-monotonic logics

In most logics, weakening is either an inference rule or a metatheorem if the logic doesn't have an explicit rule. Notable exceptions are:

• Strict logic or relevant logic, where every hypothesis must be necessary for the conclusion.
• Linear logic which disallows arbitrary contraction in addition to arbitrary weakening.
• Bunched implications where weakening is restricted to additive composition.
• Various types of default reasoning.
• Abductive reasoning, the process of deriving the most likely explanations of the known facts.
• Reasoning about knowledge, where statements specifying that something is not known need to be retracted when that thing is learned.

See also

• Contraction
• Exchange rule
• Substructural logic