Weak Hopf algebra
In mathematics, weak bialgebras are a generalization of bialgebras that are both algebras and coalgebras but for which the compatibility conditions between the two structures have been "weakened". In the same spirit, weak Hopf algebras are weak bialgebras together with a linear map S satisfying specific conditions; they are generalizations of Hopf algebras.
These objects were introduced by Böhm, Nill and Szlachányi. The first motivations for studying them came from quantum field theory and operator algebras. [1] Weak Hopf algebras have quite interesting representation theory; in particular modules over a semisimple finite weak Hopf algebra is a fusion category (which is a monoidal category with extra properties). It was also shown by Etingof, Nikshych and Ostrik that any fusion category is equivalent to a category of modules over a weak Hopf algebra. [2]
Contents |
Definition
A weak bialgebra 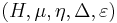 over a field
over a field  is a vector space
is a vector space  such that
such that
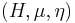 forms an associative algebra with multiplication
forms an associative algebra with multiplication 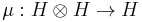 and unit
and unit 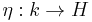 ,
,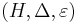 forms a coassociative coalgebra with comultiplication
forms a coassociative coalgebra with comultiplication 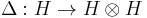 and counit
and counit 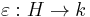 ,
,
for which the following compatibility conditions hold :
- Multiplicativity of the Coproduct :
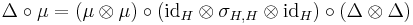 ,
,
- Weak Multiplicativity of the Counit :
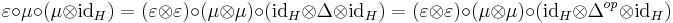 ,
,
- Weak Comultiplicativity of the Unit :
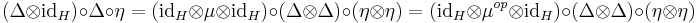 ,
,
where 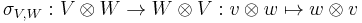 flips the two tensor factors. Moreover
flips the two tensor factors. Moreover 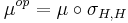 is the opposite multiplication and
is the opposite multiplication and 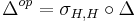 is the opposite comultiplication. Note that we also implicitly use Mac Lane's coherence theorem for the monoidal category of vector spaces, identifying
is the opposite comultiplication. Note that we also implicitly use Mac Lane's coherence theorem for the monoidal category of vector spaces, identifying 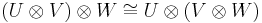 as well as
as well as 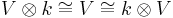 .
.
The definition is fairly self-explanatory, one sees that it is the compatibility between the algebra and coalgebra structures that is weaken.
A weak Hopf algebra 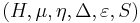 is a weak bialgebra
is a weak bialgebra 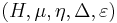 with a linear map
with a linear map 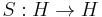 , called the antipode, that satisfies:
, called the antipode, that satisfies:
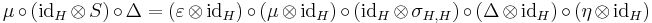 ,
,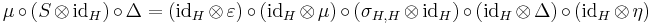 ,
,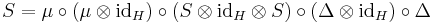 .
.
Examples
- Hopf algebra. Of course any Hopf algebra is a weak Hopf algebra.
- Groupoid algebra. Suppose
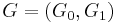 is a groupoid and let
is a groupoid and let ![K[G]](/2012-wikipedia_en_all_nopic_01_2012/I/d398bc83ba2fa89d59e6f77b4a6abca5.png) be the groupoid algebra, in other words, the algebra generated by the morphisms
be the groupoid algebra, in other words, the algebra generated by the morphisms 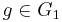 . This becomes a weak Hopf algebra if we define
. This becomes a weak Hopf algebra if we define
![\mu�: K[G] \otimes K[G] \to K[G] ~\text{by}~ \mu(g \otimes h)= \left\{ \begin{array}{cl}
g \circ h & \text{if source(h) = target(g)} \\
0 & \text{otherwise} \end{array} \right.](/2012-wikipedia_en_all_nopic_01_2012/I/b564f5f74f79139cc88c8b66e39d8af4.png)
![\eta�: k \to K[G] ~\text{by}~ \eta (1) = \sum_{X \in G_0} \mathrm{id}_X](/2012-wikipedia_en_all_nopic_01_2012/I/749bcb89b596e920af22b52163e8ef10.png)
![\Delta�: K[G] \to K[G] \otimes K[G] ~\text{by}~ \Delta(g) = g \otimes g ~ \text{for all} ~g \in G_1](/2012-wikipedia_en_all_nopic_01_2012/I/b77f346ead50802ccfb9a5b5394bcc11.png)
![\varepsilon�: K[G] \to k ~\text{by}~ \varepsilon(g) = 1 ~\text{for all}~ g \in G_1](/2012-wikipedia_en_all_nopic_01_2012/I/63561771980ecbcdeaeceee96cf5c536.png)
![S�: K[G] \to K[G] ~\text{by}~ S(g) = g^{-1} ~\text{for all}~ g \in G_1](/2012-wikipedia_en_all_nopic_01_2012/I/a4d0d9472b71285df9b546441b3b8453.png) .
.
Note that this second example is a weak Hopf algebra but not a Hopf algebra.
Representation theory
Let H be a semisimple finite weak Hopf algebra, then modules over H form a semisimple rigid monoidal category with finitely many simple objects. Moreover the homomorphisms spaces are finite-dimensional vector spaces and the endomorphisms space of simple objects are one-dimensional. Finally, the monoidal unit is a simple object. Such a category is called a fusion category.
It can be shown that some monoidal category are not modules over a Hopf algebra. In the case of fusion categories (which are just monoidal categories with extra conditions), it was proved by Etingof, Nikshych and Ostrik that any fusion category is equivalent to a category of modules over a weak Hopf algebra.
Notes
References
- Böhm, Gabriella; Nill, Florian; Szlachányi, Kornel (1999). "Weak Hops algebras. I. Integral theory and
 -stucture". Journal of Algebra 221 (2): 385–438. doi:10.1006/jabr.1999.7984.
-stucture". Journal of Algebra 221 (2): 385–438. doi:10.1006/jabr.1999.7984.
- Etingof, Pavel; Nikshych, Dimitri; Ostrik, Viktor (2005). "On fusion categories". Annals of Mathematics. Second Series 162 (2): 581–642. doi:10.4007/annals.2005.162.581.
- Karaali, Gizem (2008). "On Hopf algebras and their generalizations". Communications in Algebra 36 (12): 4341–4367. doi:10.1080/00927870802182424.