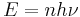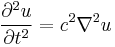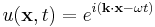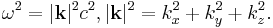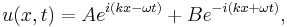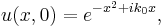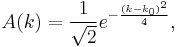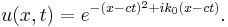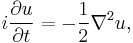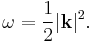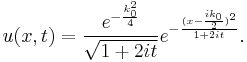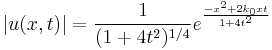Wave packet

In physics, a wave packet (or wave train) is a short "burst" or "envelope" of wave action that travels as a unit. A wave packet can be analyzed into, or can be synthesized from, an infinite set of component sinusoidal waves of different wavenumbers, with phases and amplitudes such that they interfere constructively only over a small region of space, and destructively elsewhere.[1] Depending on the evolution equation, the wave packet's envelope may remain constant (no dispersion, see figure) or it may change (dispersion) while propagating. Quantum mechanics ascribes a special significance to the wave packet: it is interpreted to be a "probability wave" describing the probability that a particle or particles in a particular state will be measured to have a given position and momentum. It is in this way similar to the wave function.

By applying the Schrödinger equation in quantum mechanics it is possible to deduce the time evolution of a system, similar to the process of the Hamiltonian formalism in classical mechanics. The wave packet is a mathematical solution to the Schrödinger equation.[2] The area under the square of the wave packet solution is interpreted to be the probability density of finding the particle in a region. The dispersive character of solutions of the Schrödinger equation has played an important role in rejecting Schrödinger's original interpretation, and accepting the Born rule.

In the coordinate representation of the wave (such as the Cartesian coordinate system) the position of the wave is given by the position of the packet. Moreover, the narrower the spatial wave packet, and therefore the better defined the position of the wave packet, the larger the spread in the momentum of the wave. This trade-off between spread in position and spread in momentum is one example of the Heisenberg uncertainty principle.

Contents

Background

In the early 1900s it became apparent that classical mechanics had some major failings. Isaac Newton originally proposed the idea that light came in discrete packets which he called "corpuscles", but the wave-like behavior of many light phenomena quickly led scientists to favor a wave description of electromagnetism. It wasn't until the 1930s that the particle nature of light really began to be widely accepted in physics. The development of quantum mechanics — and its success at explaining confusing experimental results — was at the foundation of this acceptance.

One of the most important concepts in the formulation of quantum mechanics is the idea that light comes in discrete bundles called photons. The energy of light is a discrete function of frequency:

E = nh\nu

The energy is a positive integer, n, multiple of Planck's constant, h, and frequency, ν. This resolved a significant problem in classical physics, called the ultraviolet catastrophe.

The ideas of quantum mechanics continued to be developed throughout the 20th century. The picture that was developed was of a particulate world, with all phenomena and matter made of and interacting with discrete particles; however, these particles were described by a probability wave. The interactions, locations, and all of physics would be reduced to the calculations of these probability amplitude waves. The particle-like nature of the world was significantly confirmed by experiment, while the wave-like phenomena could be characterized as consequences of the wave packet nature of particles.

Mathematics of wave packets

As an example of propagation without dispersion, consider wave solutions to the following wave equation:

{ \partial^2 u \over \partial t^2 } = c^2 { \nabla^2 u}

where c is the speed of the wave's propagation in a given medium. Using the physics time convention, 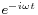\scriptstyle e^{-i \omega t}, the wave equation has plane-wave solutions

u(\bold{x},t) = e^{i{(\bold{k\cdot x}}-\omega t)}

where

\omega^2 =|\bold{k}|^2 c^2, |\bold{k}|^2 = k_x^2 %2B k_y^2%2B k_z^2.

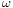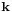This relation between \scriptstyle \omega and \scriptstyle \bold{k} should be valid so that the plane wave is a solution to the wave equation. It is called a dispersion relation.

To simplify, consider only waves propagating in one dimension (extension to three dimensions is possible). Then the general solution is

u(x,t)= A e^{i(kx-\omega t)} %2B B e^{-i(kx%2B\omega t)},\,

in which we may take 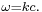\scriptstyle \omega = kc. The first term represents a wave propagating in the positive x-direction since it is a function of 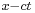\scriptstyle x - ct only; the second term, being a function of 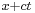\scriptstyle x %2B ct, represents a wave propagating in the negative x-direction.

A wave packet is a localized disturbance that results from the sum of many different wave forms. If the packet is strongly localized, more frequencies are needed to allow the constructive superposition in the region of localization and destructive superposition outside the region. From the basic solutions in one dimension, a general form of a wave packet can be expressed as

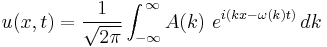u(x,t) = \frac{1}{\sqrt{2\pi}} \int^{\,\infty}_{-\infty} A(k) ~ e^{i(kx-\omega(k)t)} \,dk .

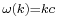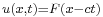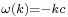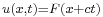Like in the plane-wave case the wave packet travels to the right for \scriptstyle \omega(k) = kc (since then \scriptstyle u(x,t) =F(x-ct)) and to the left for \scriptstyle \omega(k) = -kc (since then \scriptstyle u(x,t) = F(x%2Bct)).

The factor 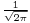\scriptstyle \frac{1}{\sqrt{2\pi}} comes from Fourier transform conventions. The amplitude 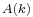\scriptstyle A(k) contains the coefficients of the linear superposition of the plane wave solutions. These coefficients can in turn be expressed as a function of 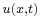\scriptstyle u(x,t) evaluated at 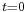\scriptstyle t=0 by inverting the Fourier transform relation above:

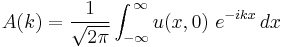A(k) = \frac{1}{\sqrt{2\pi}} \int^{\,\infty}_{-\infty} u(x,0) ~ e^{-ikx}\,dx .

For instance, choosing

u(x,0) = e^{-x^2 %2Bik_0x},

we obtain

A(k) = \frac{1}{\sqrt{2}} e^{-\frac{(k-k_0)^2}{4}},

and

u(x,t) = e^{-(x-ct)^2 %2Bik_0(x-ct)}.

The nondispersive propagation of the real or imaginary part of this wave packet is presented in the above animation.

As an example of propagation with dispersion consider solutions to the Schrödinger equation (with m and h-bar set equal to one)

i{ \partial u \over \partial t } = -\frac{1}{2} { \nabla^2 u },

yielding as dispersion relation

\omega = \frac{1}{2}|\bold{k}|^2.

Once again restricting ourselves to one dimension the solution to the Schrödinger equation satisfying the initial condition 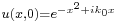\scriptstyle u(x,0) = e^{-x^2 %2Bik_0x} is found according to

u(x,t) = \frac{e^{-\frac{k_0^2}{4}}}{\sqrt{1%2B2it}}e^{-\frac{(x - \frac{ik_0}{2})^2}{1%2B2it}}.

An impression of the dispersive behaviour of this wave packet is obtained by looking at

|u(x,t)| = \frac{1}{(1%2B4t^2)^{1/4}}e^{\frac{-x^2%2B2k_0xt}{1%2B4t^2}}

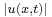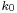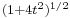(note that \scriptstyle |u(x,t)| is not a solution of the Schrödinger equation). It is seen that the dispersive wave packet, while moving with constant group velocity \scriptstyle k_0, has a time-dependent width increasing according to \scriptstyle (1%2B4t^2)^{1/2}.

See also

References

  1. ^ Joy Manners (2000). Quantum Physics: An Introduction. CRC Press. pp. 53–56. ISBN 9780750307208. http://books.google.com/books?id=LkDQV7PNJOMC&pg=PA54&dq=wave-packet+wavelengths. 
  2. ^ Toda, Mikito (2005). Geometric structures of phase space in multidimensional chaos.... Hoboken, New Jersey: John Wiley & Sons inc.. pp. 123. ISBN 0471705276. http://books.google.com/books?id=nXC1neW24qsC&pg=PA123&dq=Schr%C3%B6dinger+equation+%22wave+packet%22#v=onepage&q=&f=false.