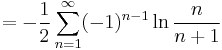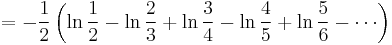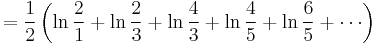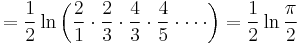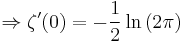Wallis product
In mathematics, Wallis' product for π, written down in 1655 by John Wallis, states that
Contents |
Derivation
Wallis derived his product as it is done in calculus books today, by comparing 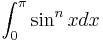 for even and odd values of n, and noting that for large n, increasing n by 1 makes little change. Since infinitesimal calculus as we know it did not yet exist then, and mathematical analysis sufficient to discuss the convergence issue was inadequate, this was a harder piece of research than it sounds with hindsight, and more tentative. Wallis's product is, in retrospect, an easy corollary of the later Euler formula for the sine function.
for even and odd values of n, and noting that for large n, increasing n by 1 makes little change. Since infinitesimal calculus as we know it did not yet exist then, and mathematical analysis sufficient to discuss the convergence issue was inadequate, this was a harder piece of research than it sounds with hindsight, and more tentative. Wallis's product is, in retrospect, an easy corollary of the later Euler formula for the sine function.
Proof using Euler's infinite product for the sine function[1]
Let x = π/2:
Proof using integral[2]
Let:
Repeating the process,
Repeating the process,
By the squeeze theorem,
Relation to Stirling's approximation
Stirling's approximation for n! asserts that
as n → ∞. Consider now the finite approximations to the Wallis product, obtained by taking the first k terms in the product:
pk can be written as
Substituting Stirling's approximation in this expression (both for k! and (2k)!) one can deduce (after a short calculation) that pk converges to π/2 as k → ∞.
ζ'(0)[1]
The Riemann zeta function and the Dirichlet eta function can be defined:
Applying an Euler transform to the latter series, the following is obtained:
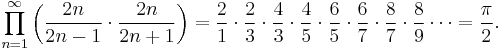
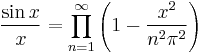
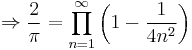
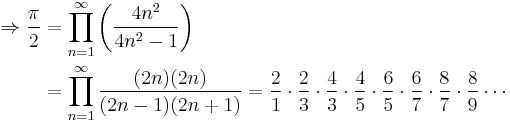
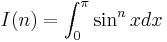
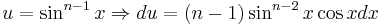
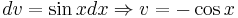
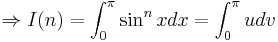
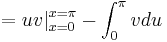
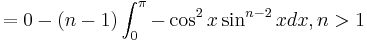
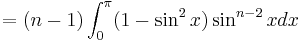
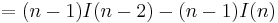
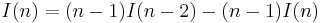
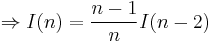
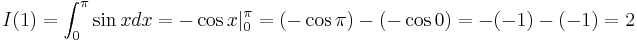
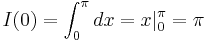
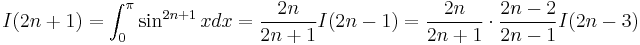

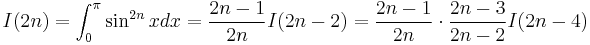

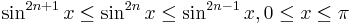
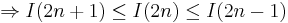
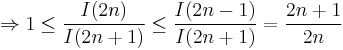
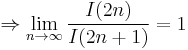
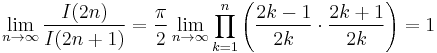
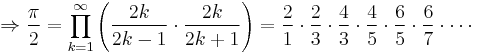
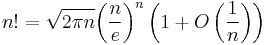
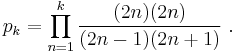
![p_k ={1\over{2k%2B1}}\prod_{n=1}^{k} \frac{(2n)^4 }{[(2n)(2n-1)]^2}={1\over{2k%2B1}}\cdot {{2^{4k}\,(k!)^4}\over {[(2k)!]^2}} \ .](/2012-wikipedia_en_all_nopic_01_2012/I/e4d226bec75893f683f0263f4db37b84.png)
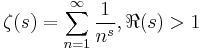
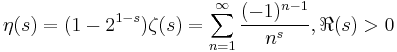
![\eta(s)=\frac{1}{2}%2B\frac{1}{2} \sum_{n=1}^\infty (-1)^{n-1}\left[\frac{1}{n^s}-\frac{1}{(n%2B1)^s}\right], \Re(s)>-1](/2012-wikipedia_en_all_nopic_01_2012/I/41b43398f90022550c68f6ec1fd9ae32.png)
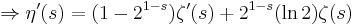
![=-\frac{1}{2} \sum_{n=1}^\infty (-1)^{n-1}\left[\frac{\ln n}{n^s}-\frac{\ln (n%2B1)}{(n%2B1)^s}\right], \Re(s)>-1](/2012-wikipedia_en_all_nopic_01_2012/I/ac94a41bc0c2d5a47ac002cf53893834.png)
![\Rightarrow \eta'(0)=-\zeta'(0)-\ln 2=-\frac{1}{2} \sum_{n=1}^\infty (-1)^{n-1}\left[\ln n-\ln (n%2B1)\right]](/2012-wikipedia_en_all_nopic_01_2012/I/80a3a9205dacd90af16540da7f2d9a85.png)