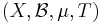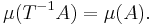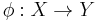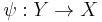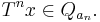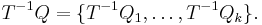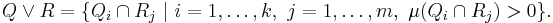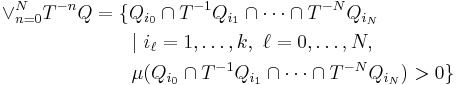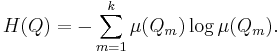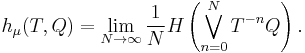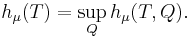Measure-preserving dynamical system
In mathematics, a measure-preserving dynamical system is an object of study in the abstract formulation of dynamical systems, and ergodic theory in particular.
Contents |
Definition
A measure-preserving dynamical system is defined as a probability space and a measure-preserving transformation on it. In more detail, it is a system
with the following structure:
 is a set,
is a set, is a σ-algebra over
is a σ-algebra over  ,
,![\mu:\mathcal{B}\rightarrow[0,1]](/2012-wikipedia_en_all_nopic_01_2012/I/e550845023c26802da3a36f74e5e98d4.png) is a probability measure, so that
is a probability measure, so that 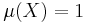 , and
, and 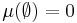
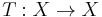 is a measurable transformation which preserves the measure
is a measurable transformation which preserves the measure  , i. e. each
, i. e. each 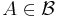 satisfies
satisfies
This definition can be generalized to the case in which  is not a single transformation that is iterated to give the dynamics of the system, but instead is a monoid (or even a group) of transformations
is not a single transformation that is iterated to give the dynamics of the system, but instead is a monoid (or even a group) of transformations 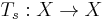 parametrized by
parametrized by 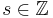 (or
(or  , or
, or 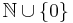 , or
, or 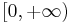 ), where each transformation
), where each transformation 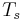 satisfies the same requirements as
satisfies the same requirements as  above. In particular, the transformations obey the rules
above. In particular, the transformations obey the rules
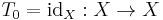 , the identity function on
, the identity function on  ;
;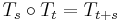 , whenever all the terms are well-defined;
, whenever all the terms are well-defined;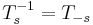 , whenever all the terms are well-defined.
, whenever all the terms are well-defined.
The earlier, simpler case fits into this framework by defining 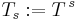 for
for 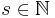 .
.
The existence of invariant measures for certain maps and Markov processes is established by the Krylov–Bogolyubov theorem.
Examples
Examples include:
- μ could be the normalized angle measure dθ/2π on the unit circle, and
 a rotation. See equidistribution theorem;
a rotation. See equidistribution theorem;
- the Bernoulli scheme;
- with the definition of an appropriate measure, a subshift of finite type;
- the base flow of a random dynamical system.
Homomorphisms
The concept of a homomorphism and an isomorphism may be defined.
Consider two dynamical systems 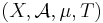 and
and 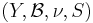 . Then a mapping
. Then a mapping
is a homomorphism of dynamical systems if it satisfies the following three properties:
- The map φ is measurable,
- For each
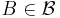 , one has
, one has 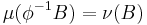 ,
, - For μ-almost all
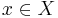 , one has
, one has  .
.
The system 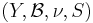 is then called a factor of
is then called a factor of 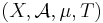 .
.
The map φ is an isomorphism of dynamical systems if, in addition, there exists another mapping
that is also a homomorphism, which satisfies
- For μ-almost all
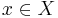 , one has
, one has 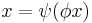
- For ν-almost all
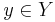 , one has
, one has 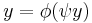 .
.
Generic points
A point 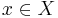 is called a generic point if the orbit of the point is distributed uniformly according to the measure.
is called a generic point if the orbit of the point is distributed uniformly according to the measure.
Symbolic names and generators
Consider a dynamical system 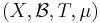 , and let Q = { Q1, ..., Qk } be a partition of X into k measurable pair-wise disjoint pieces. Given a point x ∈ X, clearly x belongs to only one of the Qi. Similarly, the iterated point T nx can belong to only one of the parts as well. The symbolic name of x, with regards to the partition Q, is the sequence of integers {an} such that
, and let Q = { Q1, ..., Qk } be a partition of X into k measurable pair-wise disjoint pieces. Given a point x ∈ X, clearly x belongs to only one of the Qi. Similarly, the iterated point T nx can belong to only one of the parts as well. The symbolic name of x, with regards to the partition Q, is the sequence of integers {an} such that
The set of symbolic names with respect to a partition is called the symbolic dynamics of the dynamical system. A partition Q is called a generator or generating partition if μ-almost every point x has a unique symbolic name.
Operations on partitions
Given a partition Q = { Q1, ..., Qk } and a dynamical system 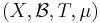 , we define T-pullback of Q as
, we define T-pullback of Q as
Further, given two partitions Q = { Q1, ..., Qk } and R = { R1, ..., Rm }, we define their refinement 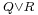 as
as
With these two constructs we may define refinement of an iterated pullback
which plays crucial role in the construction of the measure-theoretic entropy of a dynamical system.
Measure-theoretic entropy
The entropy of a partition Q is defined as
The measure-theoretic entropy of a dynamical system 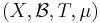 with respect to a partition Q = { Q1, ..., Qk } is then defined as
with respect to a partition Q = { Q1, ..., Qk } is then defined as
Finally, the Kolmogorov–Sinai or measure-theoretic entropy of a dynamical system 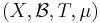 is defined as
is defined as
where the supremum is taken over all finite measurable partitions. A theorem of Yakov G. Sinai in 1959 shows that the supremum is actually obtained on partitions that are generators. Thus, for example, the entropy of the Bernoulli process is log 2, since every real number has a unique binary expansion. That is, one may partition the unit interval into the intervals [0, 1/2) and [1/2, 1]. Every real number x is either less than 1/2 or not; and likewise so is the fractional part of 2nx.
If the space X is compact and endowed with a topology, or is a metric space, then the topological entropy may also be defined.
See also
- Krylov–Bogolyubov theorem on the existence of invariant measures
- Poincaré recurrence theorem
References
- Michael S. Keane, Ergodic theory and subshifts of finite type, (1991), appearing as Chapter 2 in Ergodic Theory, Symbolic Dynamics and Hyperbolic Spaces, Tim Bedford, Michael Keane and Caroline Series, Eds. Oxford University Press, Oxford (1991). ISBN 0-19-853390-X (Provides expository introduction, with exercises, and extensive references.)
- Lai-Sang Young, "Entropy in Dynamical Systems" (pdf; ps), appearing as Chapter 16 in Entropy, Andreas Greven, Gerhard Keller, and Gerald Warnecke, eds. Princeton University Press, Princeton, NJ (2003). ISBN 0-691-11338-6
Examples
- T. Schürmann and I. Hoffmann, The entropy of strange billiards inside n-simplexes. J. Phys. A28, page 5033ff, 1995. PDF-Dokument