Volume of fluid method

In computational fluid dynamics, the volume of fluid method (or in short VOF method) is a numerical technique for tracking and locating the free surface (or fluid-fluid interface). It belongs to the class of Eulerian methods which are characterized by a mesh that is either stationary or is moving in a certain prescribed manner to accommodate the evolving shape of the interface. As such, VOF is an advection scheme—a numerical recipe that allows the programmer to track the shape and position of the interface, but it is not a standalone flow solving algorithm. The Navier-Stokes equations describing the motion of the flow have to be solved separately. The same applies for all other advection algorithms.

Contents

History

The Volume of Fluid method is based on earlier Marker-and-Cell (MAC) methods. First accounts of what is now known as VOF have been given by Noh & Woodward (1976), where fraction function C (see below) appeared, although first publication in a Journal was by Hirt & Nichols (1981). Since VOF method surpassed MAC by lowering computer storage requirements, it quickly became popular. Early applications include Torrey et al. from Los Alamos, who created VOF codes for NASA (1985,1987). First implementations of VOF suffered from imperfect interface description, which was later remedied by introducing a Piecewise-Linear Interface Calculation (PLIC) scheme . Using VOF with PLIC is a contemporary standard, used in number of computer codes [1], including ANSYS Fluent.

Specification

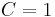The method is based on the idea of so-called fraction function C. It is defined as the integral of fluid's characteristic function in the control volume (namely, volume of a computational grid cell). Basically, when the cell is empty, with no traced fluid inside. the value of C is zero; when the cell is full, C=1; and when the interphasal interface cuts the cell, then 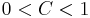0 < C < 1. C is a discontinuous function, its value jumps from 0 to 1 when the argument moves into interior of traced phase.

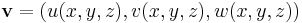The fraction function C is a scalar function, and while the fluid moves with velocity \mathbf{v}=(u(x,y,z),v(x,y,z),w(x,y,z)) (in three-dimensional space 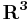\mathbf{R^3}) every fluid particle retains its identity, i.e. when a particle is a given phase, it doesn't change the phase - like a particle of air, that is a part of air bubble in water remains air particle, regardless of the bubble movement (actually, for this to hold, we have to disregard processes such as dissolving of air in water). If that is so, then the substantial derivative of fraction function C needs to be equal to zero:

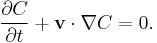
\frac{\partial C}{\partial t} %2B \mathbf{v}\cdot \nabla C =0.

This is actually the same equation that has to be fulfilled by the level set distance function \phi.

This equation cannot be easily solved directly, since C is discontinuous, but such attempts have been performed. But the most popular approach to the equation is the so called geometrical reconstruction, originating in the works of Hirt and B. D. Nichols.

The VOF method is known for its ability to conserve the "mass" of the traced fluid, also, when fluid interface changes its topology, this change is traced easily, so the interfaces can for example join, or break apart.

See also

References

  1. ^ Gerris Flow Solver (http://gfs.sourceforge.net)