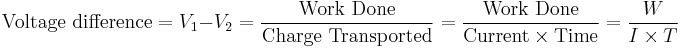Voltage
Voltage, otherwise known as electrical potential difference or electric tension (denoted ∆V and measured in volts, or joules per coulomb) is the potential difference between two points — or the difference in electric potential energy per unit charge between two points.[1] Voltage is equal to the work which would have to be done, per unit charge, against a static electric field to move the charge between two points. A voltage may represent either a source of energy (electromotive force), or it may represent lost or stored energy (potential drop). A voltmeter can be used to measure the voltage (or potential difference) between two points in a system; usually a common reference potential such as the ground of the system is used as one of the points. Voltage can be caused by static electric fields, by electric current through a magnetic field, by time-varying magnetic fields, or a combination of all three.[2][3]
Contents |
Definition
The voltage between two ends of a path is the total energy required to move a small electric charge along that path, divided by the magnitude of the charge. Mathematically this is expressed as the line integral of the electric field and the time rate of change of magnetic field along that path. In the general case, both a static (unchanging) electric field and a dynamic (time-varying) electromagnetic field must be included in determining the voltage between two points.
Historically this quantity has also been called "tension"[4] and "pressure". Pressure is now obsolete but tension is still used, for example within the phrase "high tension" (HT) which is commonly used in thermionic valve (vacuum tube) based electronics.
Voltage is defined so that negatively-charged objects are pulled towards higher voltages, while positively-charged objects are pulled towards lower voltages. Therefore, the conventional current in a wire or resistor always flows from higher voltage to lower voltage. Current can flow from lower voltage to higher voltage, but only when a source of energy is present to "push" it against the opposing electric field. For example, inside a battery, chemical reactions inside the battery provide the energy needed for current to flow from the negative terminal to the positive terminal.
Voltage may be calculated as:
Hydraulic analogy
A simple analogy for an electric circuit is water flowing in a closed circuit of pipework, driven by a mechanical pump. This can be called a water circuit. Potential difference between two points corresponds to the water pressure difference between two points. If there is a water pressure difference between two points (due to the pump), then water flowing from the first point to the second will be able to do work, such as driving a turbine. In a similar way, work can be done by the electric current driven by the potential difference due to an electric battery: for example, the current generated by an automobile battery can drive the starter motor in an automobile. If the pump isn't working, it produces no pressure difference, and the turbine will not rotate. Equally, if the automobile's battery is flat, then it will not turn the starter motor.
This water flow analogy is a useful way of understanding several electrical concepts. In such a system, the work done to move water is equal to the pressure multiplied by the volume of water moved. Similarly, in an electrical circuit, the work done to move electrons or other charge-carriers is equal to "electrical pressure" (an old term for voltage) multiplied by the quantity of electrical charge moved. Voltage is a convenient way of measuring the ability to do work. In relation to "flow", the larger the "pressure difference" between two points (potential difference or water pressure difference) the greater the flow between them (either electric current or water flow).
Applications
Specifying a voltage measurement requires explicit or implicit specification of the points across which the voltage is measured. When using a voltmeter to measure potential difference, one electrical lead of the voltmeter must be connected to the first point, one to the second point.
A common use of the term "voltage" is in describing the voltage dropped across an electrical device (such as a resistor). The voltage drop across the device can be understood as the difference between measurements at each terminal of the device with respect to a common reference point (or ground). The voltage drop is the difference between the two readings. Two points in an electric circuit that are connected by an ideal conductor without resistance and not within a changing magnetic field, have a voltage of zero. Any two points with the same potential may be connected by a conductor and no current will flow between them.
Addition of voltages
The voltage between A and C is the sum of the voltage between A and B and the voltage between B and C. The various voltages in a circuit can be computed using Kirchhoff's circuit laws.
When talking about alternating current (AC) there is a difference between instantaneous voltage and average voltage. Instantaneous voltages can be added for direct current (DC) and AC, but average voltages can be meaningfully added only when they apply to signals that all have the same frequency and phase.
Measuring instruments
Instruments for measuring voltages include the voltmeter, the potentiometer, and the oscilloscope. The voltmeter works by measuring the current through a fixed resistor, which, according to Ohm's Law, is proportional to the voltage across the resistor. The potentiometer works by balancing the unknown voltage against a known voltage in a bridge circuit. The cathode-ray oscilloscope works by amplifying the voltage and using it to deflect an electron beam from a straight path, so that the deflection of the beam is proportional to the voltage.
See also
- Alternating current (AC)
- Direct current (DC)
- Electric potential
- Electric shock
- Electrical measurements
- Electrochemical potential
- Fermi level
- High voltage
- Mains electricity (an article about domestic power supply voltages)
- Mains power systems (List of voltage by country)
- Ohm's law
- Open-circuit voltage
- Phantom voltage
- Voltage drop
References
- ^ "Voltage", Electrochemistry Encyclopedia
- ^ Demetrius T. Paris and F. Kenneth Hurd, Basic Electromagnetic Theory, McGraw-Hill, New York 1969, ISBN 0-07-048470-8, pp. 512, 546
- ^ P. Hammond, Electromagnetism for Engineers, p. 135, Pergamon Press 1969 OCLC 854336.
- ^ Tension, http://www.collinslanguage.com/results.aspx?context=3&reversed=False&action=define&homonym=0&text=tension.