Virtually
In mathematics, especially in the area of abstract algebra which studies infinite groups, the adverb virtually is used to modify a property so that it need only hold for a subgroup of finite index. Given a property P, the group G is said to be virtually P if there is a finite index subgroup H≤G such that H has property P.
Common uses for this would be when P is abelian, nilpotent, solvable or free. For example, virtually solvable groups are one of the two alternatives in the Tits alternative, while Gromov's theorem states that the finitely generated groups with polynomial growth are precisely the finitely generated virtually nilpotent groups.
This terminology is also used when P is just another group. That is, if G and H are groups then G is virtually H if G has a subgroup K of finite index in G such that K is isomorphic to H.
A consequence of this is that a finite group is virtually trivial.
Contents |
Examples
Virtually abelian
The following groups are virtually abelian.
- Any abelian group.
- Any semidirect product
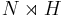 where N is abelian and H is finite. (For example, any generalized dihedral group.)
where N is abelian and H is finite. (For example, any generalized dihedral group.) - Any semidirect product
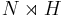 where N is finite and H is abelian.
where N is finite and H is abelian. - Any finite group (since the trivial subgroup is abelian).
Virtually nilpotent
- Any group that is virtually abelian.
- Any nilpotent group.
- Any semidirect product
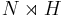 where N is nilpotent and H is finite.
where N is nilpotent and H is finite. - Any semidirect product
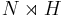 where N is finite and H is nilpotent.
where N is finite and H is nilpotent.
Virtually polycyclic
Virtually free
- Any free group.
- Any virtually cyclic group.
- Any semidirect product
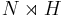 where N is free and H is finite.
where N is free and H is finite. - Any semidirect product
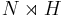 where N is finite and H is free.
where N is finite and H is free. - Any free product H * K, where H and K are both finite. (For example, the modular group PSL(2,Z).)
Others
The free group F2 on 2 generators is virtually Fn for any n ≥ 2 as a consequence of the Nielsen–Schreier theorem and the Schreier index formula.
External links
- Schreier index formula at PlanetMath.