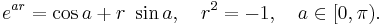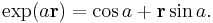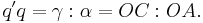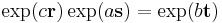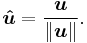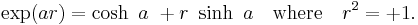Versor

In modern algebra, a versor is a quaternion of norm one. Every versor is of the form

e^{ar} = \cos a %2B r \ \sin a,\quad r^2 = -1, \quad a \in [0,\pi).

Such a versor may be viewed as a directed great-circle arc with axis r and length a. In case a = π/2, the versor is a right versor. In linear algebra, geometry, and physics, the term versor is often used for a right versor. In this case, a versor is defined as a unit vector indicating the orientation of a directed axis in a Cartesian coordinate system.

The word is from Latin versus = "turned", from pp. of vertere = "to turn", and was introduced by William Rowan Hamilton, in the context of his quaternion theory.

Contents

Presentation on the sphere

Hamilton denoted the versor of a quaternion q by the symbol Uq. He was then able to display the general quaternion in polar coordinate form

q = Tq Uq,

where Tq is the norm of q. The tensor of a versor is always equal to one. Of particular importance are the right versors, which have angle π/2. These versors have zero scalar part, and so are vectors of length one (unit vectors). The right versors form a sphere of square roots of −1 in the quaternion algebra. The generators i, j, and k in the quaternion group are examples of right versors.

If a great-circle arc has length a, and if 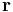\mathbf{r} is the pole of this great circle (viewed as the equator with respect to the pole), then the versor is the quaternion

\exp(a\mathbf{r}) = \cos a %2B \mathbf{r} \sin a. \,

Multiplication of quaternions of norm one corresponds to the "addition" of great circle arcs on the 2-sphere. Hamilton writes[1]

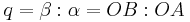q = \beta: \alpha = OB:OA \ \ and
q' = \gamma:\beta = OC:OB \,

imply

q' q = \gamma:\alpha = OC:OA . \,

The algebra of versors has been exploited to exhibit the properties of elliptic space.

Since versors correspond to elements of the 3-sphere in H, it is natural today to write

\exp(c\mathbf{r}) \exp(a\mathbf{s}) = \exp(b\mathbf{t}) \!

for the versor composition, where \mathbf{t}, is the pole of the product versor and b is its angle (as in the figure).

When we view the spherical trigonometric solution for b and 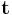\mathbf{t} in the product of exponentials, then we have an instance of the general Campbell-Baker-Hausdorff formula in Lie group theory. As the 3-sphere represented by versors in H is a 3-parameter Lie group, practice with versor compositions is good preparation for more abstract Lie group and Lie algebra theory. Indeed, as great circle arcs they compose as sums of vector arcs (Hamilton's term), but as quaternions they simply multiply. Thus the great-circle-arc model is similar to logarithm in that sums correspond to products. In Lie theory, the pair (group,algebra) carries this logarithm-likeness to higher dimensions.

Definition in linear algebra, geometry, and physics

Outside the context of quaternion theory, a versor is sometimes defined as a unit vector indicating the direction of a directed axis, or the direction of another vector. For instance:

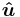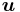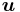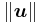  • The versor (or normalized vector) \boldsymbol{\hat{u}} of a non-zero vector \boldsymbol{u} is the unit vector codirectional with \boldsymbol{u}, i.e.,
\boldsymbol{\hat{u}} = \frac{\boldsymbol{u}}{\|\boldsymbol{u}\|}.
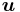where \|\boldsymbol{u}\| is the norm (or length) of \boldsymbol{u}.

Hyperbolic versor

In linear algebra, a hyperbolic versor is a quantity of the form

\exp(ar) = \cosh \ a \ %2B r\ \sinh \ a \ \ \text{ where }\ \ r^2 = %2B1.

Such elements arise in algebras of mixed signature, for example split-complex numbers or split-quaternions. It was the algebra of tessarines discovered by James Cockle in 1848 that first provided hyperbolic versors. In fact, James Cockle wrote the above equation (with r = j) when he found that the tessarines included the new type of imaginary element.

The primary exponent of hyperbolic versors was Alexander Macfarlane as he worked to shape quaternion theory to serve physical science.[2] He saw the modelling power of hyperbolic versors operating on the split-complex number plane, and in 1891 he introduced hyperbolic quaternions to extend the concept to 4-space. Problems in that algebra led to use of biquaternions after 1900. In a widely circulated review of 1899, Macfarlane said:

…the root of a quadratic equation may be versor in nature or scalar in nature. If it is versor in nature, then the part affected by the radical involves the axis perpendicular to the plane of reference, and this is so, whether the radical involves the square root of minus one or not. In the former case the versor is circular, in the latter hyperbolic.[3]

Today the concept of a one-parameter group subsumes the concepts of versor and hyperbolic versor as the terminology of Sophus Lie has replaced that of Hamilton and Macfarlane. In particular, for each r such that r r = +1 or r r = −1, the mapping 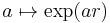a \mapsto \exp(ar) takes the real line to a group of hyperbolic or ordinary versors. In the ordinary case, when r and −r are antipodal points on a sphere, the one-parameter groups have the same points but are oppositely directed. In physics, this aspect of rotational symmetry is termed a doublet (physics).

In 1911 Alfred Robb published his Optical Geometry of Motion in which he identified the parameter rapidity which specifies a change in frame of reference. This rapidity parameter corresponds to the real variable in a one-parameter group of hyperbolic versors. With the further development of special relativity the action of a hyperbolic versor came to be called a Lorentz boost.

See also

References

  1. ^ Elements of Quaternions, 2nd edition,v.1,p.146
  2. ^ Papers on Space Analysis (1894), papers 2,3, and 5, see external link below.
  3. ^ Science, 9:326 (1899)

External links