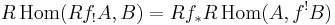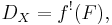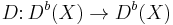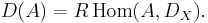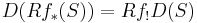Verdier duality

For duality over number fields, see Artin–Verdier duality.

In mathematics, Verdier duality is a generalization of the Poincaré duality of manifolds to locally compact spaces with singularities. Verdier duality was introduced by Verdier (1967, 1995), as an analog for locally compact spaces of the coherent duality for schemes due to Grothendieck. It plays a role in the theory of perverse sheaves.

1 Notation
2 Verdier duality
3 Poincaré duality
4 References

Notation

Image functors for sheaves
direct image f_∗
inverse image f^∗
direct image with compact support f_!
exceptional inverse image Rf^!
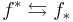$f^* \leftrightarrows f_*$
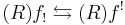$(R)f_! \leftrightarrows (R)f^!$

F is a field.
The dimension of a locally compact space is the smallest integer n such that H_cⁿ⁺¹(X,S) = 0 for all abelian sheaves S (or infinity if no such integer n exists).
X and Y are finite dimensional locally compact spaces, and f is a continuous map from X to Y.
[A,B] is the set of morphisms between elements A and B of the derived category of sheaves on a space.
f_∗ and f^∗ are the usual direct and inverse image functors between sheaves induced by f. The functor f^∗ is the left adjoint of f_∗.
f_! is the direct image with compact support and Rf^! is the exceptional inverse image functor.

The exclamation mark is often pronounced "shriek" (slang for exclamation mark), and the maps called "f shriek" or "f lower shriek" and "f upper shriek" – see also shriek map.

Verdier duality

Global Verdier duality states that Rf_! has a right adjoint f^! in the derived category, in other words

$[Rf_!A,B] = [A,f^!B] . \,\!$

If X is a finite covering space of Y then f^! takes sheaves to sheaves and is the same as f^∗. If X is a closed subspace of Y then f^! again takes sheaves to sheaves, but in general its image on sheaves cannot be represented by a single sheaf, but only by a complex of sheaves on the derived category.

Local Verdier duality states that

$R\,\mathrm{Hom}(Rf_!A,B) = Rf_{\ast}R\,\mathrm{Hom}(A,f^!B)$

in the right derived category of sheaves of F modules over X. Taking homology of both sides gives global Verdier duality.

The dualizing complex D_X on X is defined to be

$D_X = f^!(F) , \,\!$

where f is the map from X to a point.

If X is a finite dimensional locally compact space, and D^b(X) the bounded derived category of sheaves of abelian groups over X, then the Verdier dual is a contravariant functor

$D \colon D^b(X)\to D^b(X) \,\!$

defined by

$D(A) = R\,\mathrm{Hom}(A, D_X) . \,\!$

It has the following properties:

D²(S) is isomorphic to S when S has constructible cohomology.
(Verdier duality) If f is a continuous map from X to Y then there is an isomorphism

$D(Rf_{\ast}(S)) = Rf_!D(S)$

for any S ∈ D^b(X).

Here Rf_∗ denotes the higher direct image, at the derived category level.

In the special case when Y is a point and X is compact this says (roughly) that the cohomologies of dual complexes are dual.

Poincaré duality

Poincaré duality is a special case of Verdier duality; this can be seen as follows.

In the derived category, cohomology can be interpreted as chain homotopy classes of maps

H^k (X, F) = [F[−k],X] = [F, X[k]]

where F[−k] is the complex with the constant sheaf F concentrated in degree k, and [—, —] denote the chain homotopy classes of maps. The Verdier dual allows us to interpret homology in the derived category as well:

[F[−k], D_X] = H_k (X, F).

The left hand side is by definition the dual of the cohomology with compact support, so this equation says that homology is dual to cohomology with compact support.

It also follows that for an oriented manifold M, the Verdier dual is given by

D_M = F[−n].

Ordinary Poincaré duality of a manifold can then be interpreted as the perfect pairing

[F[−k], F] ⊗ [F[k−n], F[[−n]] → [F[−n], F[[−n]] → F.

References

Borel, Armand (1984), Intersection cohomology, Progress in Mathematics, Basel, Boston, Berlin: Birkhäuser, ISBN 978-0-8176-3274-8
Gelfand, Sergei I.; Manin, Yuri Ivanovich (1999), Homological algebra, Berlin: Springer, ISBN 978-3-540-65378-3
Grothendieck, Alexandre (1977), Séminaire de Géométrie Algébrique du Bois Marie - 1965-66 - Cohomologie l-adique et Fonctions L - (SGA 5), Lecture notes in mathematics, 589, Berlin, New York: Springer-Verlag, pp. xii+484, ISBN 978-3-540-08248-4 , Exposés I and II contain the corresponding theory in the étale situation
Iversen, Birger (1986), Cohomology of sheaves, Universitext, Berlin, New York: Springer-Verlag, ISBN 978-3-540-16389-3, MR 842190
Verdier, Jean-Louis (1967), "A duality theorem in the etale cohomology of schemes", in Springer, Tonny Albert, Proceedings of a Conference on Local Fields: NUFFIC Summer School held at Driebergen (The Netherlands) in 1966, Berlin, New York: Springer-Verlag, pp. 184–198, ISBN 978-3-540-03953-2, MR 0230732, http://books.google.com/books?id=SW-mAAAAIAAJ
Verdier, Jean-Louis (1995), "Dualité dans la cohomologie des espaces localement compacts", Séminaire Bourbaki, Vol. 9, Paris: Société Mathématique de France, pp. Exp. No. 300, 337–349, ISBN 978-2-85629-042-2, MR 1610971, http://www.numdam.org/item?id=SB_1964-1966__9__337_0

Verdier duality

Contents

Notation

Verdier duality

Poincaré duality

References