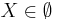Urelement
In set theory, a branch of mathematics, an urelement or ur-element (from the German prefix ur-, 'primordial') is an object (concrete or abstract) which is not a set, but that may be an element of a set. Urelements are sometimes called "atoms" or "individuals."
Contents |
Theory
There are several different but essentially equivalent ways to treat urelements in a first-order theory.
One way is to work in a first-order theory with two sorts, sets and urelements, with a ∈ b only defined when b is a set. In this case, if U is an urelement, it makes no sense to say
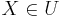 ,
,
although
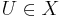 ,
,
is perfectly legitimate.
This should not be confused with the empty set where saying
is well-formed but false.
Another way is to work in a one-sorted theory with a unary relation used to distinguish sets and urelements. As non-empty sets contain members while urelements do not, the unary relation is only needed to distinguish the empty set from urelements. Note that in this case, the axiom of extensionality must be formulated to apply only to objects that are not urelements.
This situation is analogous to the treatments of theories of sets and classes. Indeed, urelements are in some sense dual to proper classes: urelements cannot have members whereas proper classes cannot be members. Put differently, urelements are minimal objects while proper classes are maximal objects by the membership relation (which, of course, is not an order relation, so this analogy is not to be taken literally.)
Urelements in set theory
The Zermelo set theory of 1908 included urelements. It was soon realized that in the context of this and closely related axiomatic set theories, the urelements were not needed because they can easily be modeled in a set theory without urelements. Thus standard expositions of the canonical axiomatic set theories ZF and ZFC do not mention urelements. (For an exception, see Suppes.[1]) Axiomatizations of set theory that do invoke urelements include Kripke–Platek set theory with urelements, and the variant of Von Neumann–Bernays–Gödel set theory described by Mendelson.[2] In type theory, an object of type 0 can be called an urelement; hence the name "atom."
Adding urelements to the system New Foundations (NF) to produce NFU has surprising consequences. In particular, Jensen proved[3] the consistency of NFU relative to Peano arithmetic; meanwhile, the consistency of NF relative to anything remains an open problem. Moreover, NFU remains relatively consistent when augmented with an axiom of infinity and the axiom of choice. Meanwhile, the negation of the axiom of choice is, curiously, an NF theorem. Holmes (1998) takes these facts as evidence that NFU is a more successful foundation for mathematics than NF. Holmes further argues that set theory is more natural with than without urelements, since we may take as urelements the objects of any theory or of the physical universe.[4]
References
- ^ Patrick Suppes (1960) Axiomatic Set Theory. Van Nostrand. Dover reprint, 1972.
- ^ Mendelson, Elliot (1997: 297–304) Introduction to Mathematical Logic, 4th ed. London: Chapman & Hall
- ^ Ronald Jensen (1969) "On the Consistency of a Slight(?) Modification of Quine's NF," Synthese 19: 250–63
- ^ Holmes, Randall, 1998. Elementary Set Theory with a Universal Set. Academia-Bruylant.
External links
- Weisstein, Eric W., "Urelement" from MathWorld.