Upsampling

Upsampling is the process of increasing the sampling rate of a signal. For instance, upsampling raster images such as photographs means increasing the resolution of the image.

The upsampling factor (commonly denoted by L) is usually an integer or a rational fraction greater than unity. This factor multiplies the sampling rate or, equivalently, divides the sampling period. For example, if compact disc audio is upsampled by a factor of 5/4 then the resulting sampling rate goes from 44,100 Hz to 55,125 Hz.

Contents

Filtering

For an aesthetically pleasing upsample, an interpolation filter is required; in both upsampling and downsampling, such a low-pass filter implements anti-aliasing.

Upsampling process

Consider a discrete signal 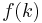f(k) on a radian frequency digital frequency range.

Upsampling by integer factor

Let L denote the upsampling factor.

  1. Add L-1 zeros between each sample in 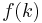f(k). Or, equivalently define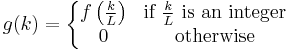 g(k) = \left \{ \begin{matrix} f\left(\frac{k}{L}\right) & \mbox{if } \frac{k}{L} \mbox{ is an integer} \\ 0 & \mbox{otherwise} \end{matrix} \right.
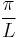
  2. Filter with a low-pass filter which, theoretically, should be the sinc filter with frequency cut off at \frac{\pi}{L}

The second step calls for the use of a perfect low-pass filter, which is not implementable. When choosing a realizable low-pass filter this will have to be considered and it will have aliasing effects. These aliases can be removed to a reasonable extent by a finite impulse response low pass filter. The presence of zeros in the sequence which is passed through the filter can be used to reduce the complexity of the filter implementation. The original filter can be split to L subfilters and the output of each of these subfilters is sequentially tapped to obtain the filtered output sequence.

Upsampling by rational fraction

Let L/M denote the upsampling factor.

  1. Upsample by a factor of L
  2. Downsample by a factor of M

Note that upsampling requires an interpolation filter after increasing the data rate and that downsampling requires a filter before decimation. These two filters can be combined into a single filter. Since both interpolation and anti-aliasing filters are low-pass filters, the filter with the smallest bandwidth is more restrictive and, thus, can be used in place of both filters. Since the rational fraction L/M is greater than unity when 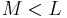M < L, the single low-pass filter should have cutoff at 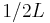1/{2L} cycles per intermediate sample, the Nyquist frequency of the input sample rate.

See also

References

Theory
Sub-fields
Techniques
Sampling