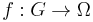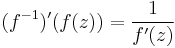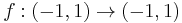Univalent function

In mathematics, in the branch of complex analysis, a holomorphic function on an open subset of the complex plane is called univalent if it is one-to-one.

1 Examples
2 Basic properties
3 Comparison with real functions
4 References

Examples

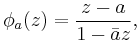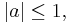Any mapping $\phi_a$ of the open unit disc to itself, : $\phi_a(z) =\frac{z-a}{1 - \bar{a}z},$ where $|a|\le 1,$ is univalent.

Basic properties

One can prove that if $G$ and $\Omega$ are two open connected sets in the complex plane, and

$f: G \to \Omega$

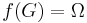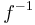is a univalent function such that $f(G) = \Omega$ (that is, $f$ is onto), then the derivative of $f$ is never zero, $f$ is invertible, and its inverse $f^{-1}$ is also holomorphic. More, one has by the chain rule

$(f^{-1})'(f(z)) = \frac{1}{f'(z)}$

for all $z$ in $G.$

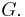
Comparison with real functions

For real analytic functions, unlike for complex analytic (that is, holomorphic) functions, these statements fail to hold. For example, consider the function

$f: (-1, 1) \to (-1, 1) \,$

given by ƒ(x) = x³. This function is clearly one-to-one, however, its derivative is 0 at x = 0, and its inverse is not analytic, or even differentiable, on the whole interval (−1, 1).

References

John B. Conway. Functions of One Complex Variable I. Springer-Verlag, New York, 1978. ISBN 0-387-90328-3.

John B. Conway. Functions of One Complex Variable II. Springer-Verlag, New York, 1996. ISBN 0-387-94460-5.

This article incorporates material from univalent analytic function on PlanetMath, which is licensed under the Creative Commons Attribution/Share-Alike License.

Univalent function

Contents

Examples

Basic properties

Comparison with real functions

References