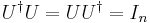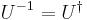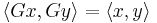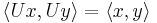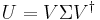Unitary matrix

In mathematics, a unitary matrix is a (square) 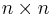$n\times n$ complex matrix $U$ satisfying the condition

$U^{\dagger} U = UU^{\dagger} = I_n\,$

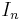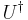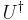
where $I_n$ is the identity matrix in n dimensions and $U^{\dagger}$ is the conjugate transpose (also called the Hermitian adjoint) of $U$ . Note this condition implies that a matrix $U$ is unitary if and only if it has an inverse which is equal to its conjugate transpose $U^{\dagger} \,$

$U^{-1} = U^{\dagger} \,\;$

A unitary matrix in which all entries are real is an orthogonal matrix. Just as an orthogonal matrix $G$ preserves the (real) inner product of two real vectors,

$\langle Gx, Gy \rangle = \langle x, y \rangle$

so also a unitary matrix $U$ satisfies

$\langle Ux, Uy \rangle = \langle x, y \rangle$

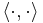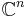for all complex vectors x and y, where $\langle\cdot,\cdot\rangle$ stands now for the standard inner product on $\mathbb{C}^n$ .

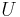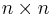If $U \,$ is an $n\times n$ matrix then the following are all equivalent conditions:

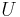$U \,$ is unitary
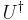$U^{\dagger} \,$ is unitary
the columns of 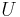$U \,$ form an orthonormal basis of 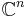$\mathbb{C}^n$ with respect to this inner product
the rows of 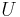$U \,$ form an orthonormal basis of 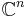$\mathbb{C}^n$ with respect to this inner product
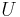$U \,$ is an isometry with respect to the norm from this inner product
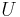$U \,$ is a normal matrix with eigenvalues lying on the unit circle.

1 Properties
2 See also
3 References
4 External links

Properties

All unitary matrices are normal, and the spectral theorem therefore applies to them. Thus every unitary matrix $U$ has a decomposition of the form

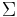$U = V\Sigma V^{\dagger}\;$

where $V$ is unitary, and $\Sigma$ is diagonal and unitary. That is, a unitary matrix is diagonalizable by a unitary matrix.

For any unitary matrix $U$ , the following hold:

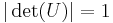$|\det(U)|=1$ .
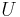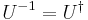$U \,$ is invertible, with $U^{-1}=U^{\dagger}$ .
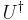$U^{\dagger}\,$ is also unitary.
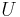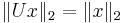$U \,$ preserves length ("isometry"): $\|Ux\|_2=\|x\|_2$ .
if 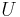$U \,$ has complex eigenvalues, they are of modulus 1. ^[1]
Eigenspaces are Orthogonal: If matrix is normal then its eigenvectors corresponding to different eigenvalues are orthogonal.
For any n, the set of all n by n unitary matrices with matrix multiplication forms a group, called U(n).
Any unit-norm matrix is the average of two unitary matrices. As a consequence, every 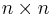$n \times n$ matrix is a linear combination of two unitary matrices.^[2]

References

^ Shankar, R.. Principles of Quantum Mechanics (2nd ed.). p. 39. ISBN 0306403978.
^ Li, Chi-Kwong; Poon, Edward. Additive Decomposition of Real Matrices. p. 1.

External links

Weisstein, Eric W., "Unitary Matrix" from MathWorld.
Ivanova, O. A. (2001), "Unitary matrix", in Hazewinkel, Michiel, Encyclopedia of Mathematics, Springer, ISBN 978-1556080104, http://www.encyclopediaofmath.org/index.php?title=U/u095540

Unitary matrix

Contents

Properties

See also

References

External links