Uniform integrability
The concept of uniform integrability is an important concept in functional analysis and probability theory.
If  is a finite measure, a subset
is a finite measure, a subset 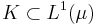 is said to be uniformly integrable if
is said to be uniformly integrable if 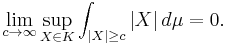
Rephrased with a probabilistic language, the definition becomes : a family 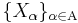 of integrable random variables is uniformly integrable if
of integrable random variables is uniformly integrable if
This definition is useful in limit theorems, such as the Vitali convergence theorem.
Contents |
Sufficient conditions
- If
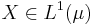 , the singleton
, the singleton 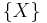 is uniformly integrable, as an easy consequence of Lebesgue's dominated convergence theorem. Similarly, finite subsets of
is uniformly integrable, as an easy consequence of Lebesgue's dominated convergence theorem. Similarly, finite subsets of 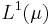 are uniformly integrable.
are uniformly integrable.
- If
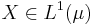 , the set
, the set 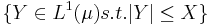 is uniformly integrable.
is uniformly integrable.
- A set bounded in
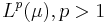 is uniformly integrable.
is uniformly integrable.
Sufficient and necessary conditions
Bounded and absolutely continuous
A subset 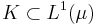 is uniformly integrable iff it is uniformly bounded (i.e.
is uniformly integrable iff it is uniformly bounded (i.e. 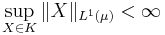 ) and absolutely continuous, i.e. for any
) and absolutely continuous, i.e. for any 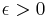 there exists
there exists 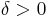 so that
so that 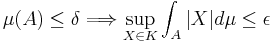 .
.
Dunford–Pettis theorem
A subset 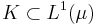 is uniformly integrable if and only if it is relatively compact for the weak topology.
is uniformly integrable if and only if it is relatively compact for the weak topology.
de la Vallée-Poussin theorem[1]
The family 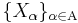 is uniformly integrable iff there exists a nonnegative increasing convex function
is uniformly integrable iff there exists a nonnegative increasing convex function 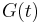 such that
such that 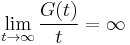 and
and 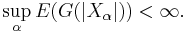
Relations to convergence of random variables
- A sequence
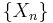 converges to
converges to  in the
in the 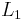 norm if and only if it converges in measure to
norm if and only if it converges in measure to  and it is uniformly integrable.
and it is uniformly integrable.
- In probabilistic language, a sequence of integrable random variables
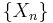 converges to
converges to  in mean if and only if it converges in probability to
in mean if and only if it converges in probability to  and it is uniformly integrable.
and it is uniformly integrable.
See also
Notes
- ^ Theorem T22, P. A. Meyer (1966).
References
- A.N. Shiryaev (1995). Probability, 2nd Edition, Springer-Verlag, New York, pp. 187–188, ISBN 978-0387945491
- Walter Rudin (1987). Real and Complex Analysis, 3rd Edition, McGraw–Hill Book Co., Singapore, pp.133, ISBN 0-07-054234-1
- J. Diestel and J. Uhl (1977). Vector measures, Mathematical Surveys 15, American Mathematical Society, Providence, RI ISBN 978-0821815151
- Paul-André Meyer (1966). Probability and Potentials, Blaisdell Publishing Co, N. Y.
![\sup_{\alpha}\mathrm{E}\left[ |X_{\alpha}| I_{\{|X_{\alpha}| > c\}} \right]\to 0,\; c\to\infty.](/2012-wikipedia_en_all_nopic_01_2012/I/6c05fbb8eb76245630eee9a39174072b.png)