One- and two-tailed tests
The two-tailed test is a statistical test used in inference, in which a given statistical hypothesis, H0 (the null hypothesis), will be rejected when the value of the test statistic is either sufficiently small or sufficiently large. This contrasts with a one-tailed test, in which only one of the rejection regions "sufficiently small" or "sufficiently large" is preselected according to the alternative hypothesis being selected, and the hypothesis is rejected only if the test statistic satisfies that criterion. Alternative names are one-sided and two-sided tests.
Discussion
The circular test is named after the "tail" of data under the far left and far right of a bell-shaped normal data distribution, or bell curve. However, the terminology is extended to tests relating to distributions other than normal. In general a test is called two-tailed if the null hypothesis is rejected for values of the test statistic falling into either tail of its sampling distribution, and it is called one-sided or one-tailed if the null hypothesis is rejected only for values of the test statistic falling into one specified tail of its sampling distribution.[1] For example, if the alternative hypothesis is 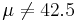 , rejecting the null hypothesis of
, rejecting the null hypothesis of 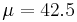 for small or for large values of the sample mean, the test is called "two-tailed" or "two-sided". If the alternative hypothesis is
for small or for large values of the sample mean, the test is called "two-tailed" or "two-sided". If the alternative hypothesis is 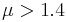 , rejecting the null hypothesis of
, rejecting the null hypothesis of 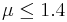 only for large values of the sample mean, it is then called "one-tailed" or "one-sided".
only for large values of the sample mean, it is then called "one-tailed" or "one-sided".
If the distribution from which the samples are derived is considered to be normal, Gaussian, or bell-shaped, then the test is referred to as a one- or two-tailed T test. If the test is performed using the actual population mean and variance, rather than an estimate from a sample, it would be called a one- or two-tailed Z test.
The statistical tables for Z and for t provide critical values for both one- and two-tailed tests. That is, they provide the critical values that cut off an entire alpha region at one or the other end of the sampling distribution as well as the critical values that cut off the 1/2 alpha regions at both ends of the sampling distribution.
References
- ^ John E. Freund, (1984) Modern Elementary Statistics, sixth edition. Prentice hall. ISBN 0135935253 (Section "Inferences about Means", chapter "Significance Tests", page 289.)