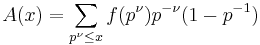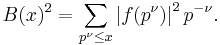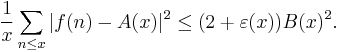Turán–Kubilius inequality
The Turán–Kubilius inequality is a mathematical theorem in probabilistic number theory. It is useful for proving results about the normal order of an arithmetic function.[1]:305–308 The theorem was proved in a special case in 1934 by Paul Turán and generalized in 1956 and 1964 by Jonas Kubilius.[1]:316
Statement of the theorem
This formulation is from Tenenbaum.[1]:302 Other formulations are in Narkiewicz[2]:243 and in Cojocaru & Murty.[3]:45–46
Suppose f is an additive complex-valued arithmetic function, and write p for an arbitrary prime and ν for an arbitrary positive integer. Write
and
Then there is a function ε(x) that goes to zero when x goes to infinity, and such that for x ≥ 2 we have
Applications of the theorem
Turán developed the inequality to create a simpler proof of the Hardy–Ramanujan theorem about the normal order of the number ω(n) of distinct prime divisors of an integer n.[1]:316 There is an exposition of Turán's proof in Hardy & Wright, §22.11.[4] Tenenbaum[1]:305–308 gives a proof of the Hardy–Ramanujan theorem using the Turán–Kubilus inequality and states without proof several other applications.
Notes
- ^ a b c d e Tenenbaum, Gérald (1995). Introduction to Analytic and Probabilistic Number Theory. Cambridge studies in advanced mathematics. 46. Cambridge University Press. ISBN 0-521-41261-7.
- ^ Narkiewicz, Władysław (1983). Number Theory. Singapore: World Scientific. ISBN 9789971950132. http://books.google.com/books?id=4CUUmYrem2YC.
- ^ Cojocaru, Alina Carmen; Murty, M. Ram (2005). An Introduction to Sieve Methods and Their Applications. London Mathematical Society Student Texts. 66. Cambridge University Press. ISBN 0-521-61275-6.
- ^ Hardy, G. H.; Wright, E. M. (2008) [First edition 1938]. An Introduction to the Theory of Numbers. Revised by D. R. Heath-Brown and Joseph H. Silverman (Sixth ed.). Oxford, Oxfordshire: Oxford University Press. ISBN 9780199219865.