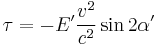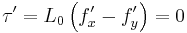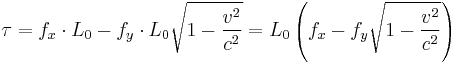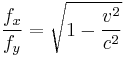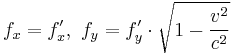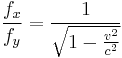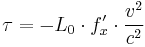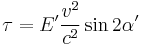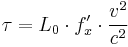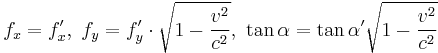Trouton–Noble experiment
The Trouton–Noble experiment (also connected to thought experiments such as the "Trouton-Noble paradox", "Right-angle lever paradox", or "Lewis-Tolman paradox") attempted to detect motion of the Earth through the luminiferous aether, and was conducted in 1901–1903 by Frederick Thomas Trouton (who also developed the Trouton's ratio) and H. R. Noble. It was based on a suggestion by George FitzGerald that a charged parallel-plate capacitor moving through the aether should orient itself perpendicular to the motion. Like the earlier Michelson–Morley experiment, Trouton and Noble obtained a null result: no motion relative to the aether could be detected.[1] [2]
This null result was reproduced, with increasing sensitivity, by Rudolf Tomaschek (1925, 1926), Chase (1926, 1927) and Hayden in 1994. [3] [4] [5] [6] [7] [8] Such experimental results are now seen, consistent with special relativity, to reflect the validity of the principle of relativity and the absence of any absolute rest frame (or aether). See also Tests of special relativity.
Contents |
Trouton–Noble Experiment
In the experiment, a suspended parallel-plate capacitor is held by a fine torsion fiber and is charged. If the aether theory were correct, the change in Maxwell's equations due to the Earth's motion through the aether would lead to a torque causing the plates to align perpendicular to the motion. This is given by:
where  is the torque,
is the torque,  the energy of the condenser,
the energy of the condenser,  the angle between the normal of the plate and the velocity.
the angle between the normal of the plate and the velocity.
On the other hand, the assertion of special relativity that Maxwell's equations are invariant for all frames of reference moving at constant velocities would predict no torque (a null result). Thus, unless the aether were somehow fixed relative to the Earth, the experiment is a test of which of these two descriptions is more accurate. Its null result thus confirms Lorentz invariance of special relativity.
However, while the negative experimental outcome can easily be explained in the rest frame of the device, the explanation from the viewpoint of a non-co-moving frame (concerning the question, whether the same torque should arise as in the "aether frame" described above, or whether no torque arises at all) is much more difficult and is called "Trouton-Noble paradox".
Right-angle lever paradox.
The Trouton–Noble paradox is essentially equivalent to a thought experiment called "right angle lever paradox", first discussed by Gilbert Newton Lewis and Richard Chase Tolman in 1909.[9] Suppose a right-angle lever with endpoints abc. In its rest frame, the forces 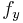 towards ba and
towards ba and 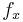 towards bc must be equal to obtain equilibrium, thus no torque is given by the law of the lever:
towards bc must be equal to obtain equilibrium, thus no torque is given by the law of the lever:
where  is the torque, and
is the torque, and 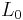 the rest length of one lever arm. However, due to length contraction, ba is longer than bc in a non-co-moving system, thus the law of the lever gives:
the rest length of one lever arm. However, due to length contraction, ba is longer than bc in a non-co-moving system, thus the law of the lever gives:
It can be seen that the torque is not zero, which apparently would cause the lever to rotate in the non-co-moving frame. Since no rotation is observed, Lewis and Tolman thus concluded that no torque exists, therefore:
However, as shown by Max von Laue (1911),[10] this is in contradiction with the relativistic expressions of force,
which gives
When applied to the law of the lever, the following torque is produced:
Which is principally the same problem as in the Trouton-Noble paradox.
Solutions
The detailed relativistic analysis of both the Trouton-Noble paradox and the Right-angle lever paradox requires care to correctly reconcile, for example, the effects seen by observers in different frames of reference, but ultimately all such theoretical descriptions are shown to give the same result. In both cases an apparent net torque on an object (when viewed from a certain frame of reference) does not result in any rotation of the object, and in both cases this is explained by correctly accounting, in the relativistic way, for the transformation of all the relevant forces, momenta and the accelerations produced by them. The early history of descriptions of this experiment is reviewed by Janssen (1995).
Laue current
The first solution of the Trouton-Noble paradox was given by Hendrik Lorentz (1904). His result is based on the assumption, that the torque and momentum due to electrostatic forces, is compensated by the torque and momentum due to molecular forces.[11]
This was further elaborated by Max von Laue (1911), who gave the standard solution for these kind of paradoxes. It was based on the so called "inertia of energy" in its general formulation by Max Planck. According to Laue, an energy current connected with a certain momentum ("Laue current") is produced in moving bodies by elastic stresses. The resulting mechanical torque in the case of the Trouton-Noble experiment amounts to:
and in the right-angle lever:
which exactly compensates the electromagnetic torque mentioned above, thus no rotation occurs on both cases. Or in other words: The electromagnetic torque is actually necessary for the uniform motion of a body, i.e., to hinder the body to rotate due to the mechanical torque caused by elastic stresses.[12] [10] [13] [14]
Since then, many papers appeared which elaborated on Laue's current and provided some modifications or re-interpretations. Other authors criticized Laue's solution, and tried to find another solution by redefining the concepts of force, equilibrium etc. (see the list at "further reading" below.)
Force and Acceleration
A solution without using compensating forces, and without the need of redefining the relativistic concepts of force, equilibrium etc., was published by Paul Sophus Epstein (1911).[15][16] He alluded to the fact that force and acceleration not always have the same direction, that is, the relation of mass, force and acceleration has tensor character in relativity. So the role played by the concept of force in relativity is very different from that of Newtonian mechanics.
Epstein imagined a massless rod with endpoints OM, which is mounted at point O, and a particle with rest mass m is mounted at M. The rod encloses the angle 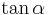 with O. Now a force towards OM is applied at M, and equilibrium in its rest frame is achieved when
with O. Now a force towards OM is applied at M, and equilibrium in its rest frame is achieved when 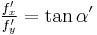 . As already shown above, these forces have the form in a non-co-moving frame:
. As already shown above, these forces have the form in a non-co-moving frame:
Thus 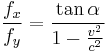 .
.
So the resultant force does not directly point from O to M. Does this lead to a rotation of the rod? No, because Epstein now considered the accelerations caused by the two forces. The relativistic expressions in the case, where a mass m is accelerated by these two forces in the longitudinal and transverse direction, are:
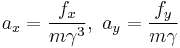 , where
, where 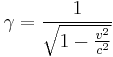 .
.
Thus 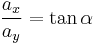 .
.
Thus no rotation occurs in this system as well. Similar considerations are also to be applied to the right-angle lever and Trouton-Noble paradox. So the paradoxes are resolved, because the two accelerations (as vectors) point to the center of gravity of the system (condenser), although the two forces do not.
Epstein added, that if one finds it more satisfying to re-establish the parallelism between force and acceleration with which we are accustomed in Newtonian mechanics, one has to include a compensating force, which formally corresponds to Laue's current. Epstein developed such a formalism in the subsequent sections of his 1911 paper.
See also
References
- ^ F. T. Trouton and H. R. Noble, "The mechanical forces acting on a charged electric condenser moving through space," Phil. Trans. Royal Soc. A 202, 165–181 (1903).
- ^ F. T. Trouton and H. R. Noble, "The Forces Acting on a Charged Condenser moving through Space. Proc. Royal Soc. 74 (479): 132-133 (1903).
- ^ R. Tomaschek (1925). "Über Versuche zur Auffindung elektrodynamischer Wirkungen der Erdbewegung in großen Höhen I". Annalen der Physik 78: 743–756. http://gallica.bnf.fr/ark:/12148/bpt6k15380p/f765.image.
- ^ R. Tomaschek (1926). "Über Versuche zur Auffindung elektrodynamischer Wirkungen der Erdbewegung in großen Höhen II". Annalen der Physik 80: 509–514. http://gallica.bnf.fr/ark:/12148/bpt6k15382c/f533.image.
- ^ Carl T. Chase (1926). "A Repetition of the Trouton-Noble Ether Drift Experiment". Physical Review 28 (2): 378–383. Bibcode 1926PhRv...28..378C. doi:10.1103/PhysRev.28.378.
- ^ Carl T. Chase (1927). "The Trouton–Noble Ether Drift Experiment". Physical Review 30 (4): 516–519. Bibcode 1927PhRv...30..516C. doi:10.1103/PhysRev.30.516.
- ^ R. Tomaschek (1927). "Bemerkung zu meinen Versuchen zur Auffindung elektrodynamischer Wirkungen in großen Höhen". Annalen der Physik 84: 161–162. http://gallica.bnf.fr/ark:/12148/bpt6k15386r/f170.image.
- ^ H. C. Hayden (1994). "High sensitivity Trouton–Noble experiment". Rev. Scientific Instruments 65 (4): 788–792. Bibcode 1994RScI...65..788H. doi:10.1063/1.1144955.
- ^ Lewis, Gilbert N. & Tolman, Richard C. (1909), "The Principle of Relativity, and Non-Newtonian Mechanics", Proceedings of the American Academy of Arts and Sciences 44: 709–726
- ^ a b Laue, Max von (1911). "Ein Beispiel zur Dynamik der Relativitätstheorie". Verhandlungen der Deutschen Physikalischen Gesellschaft 13: 513–518.
-
- English Wikisource translation: An Example Concerning the Dynamics of the Theory of Relativity
-
- ^ Lorentz, Hendrik Antoon (1904), "Electromagnetic phenomena in a system moving with any velocity smaller than that of light", Proceedings of the Royal Netherlands Academy of Arts and Sciences 6: 809–831
- ^ Laue, Max von (1911). "Zur Dynamik der Relativitätstheorie". Annalen der Physik 340 (8): 524–542. Bibcode 1911AnP...340..524L. doi:10.1002/andp.19113400808.
-
- English Wikisource translation: On the Dynamics of the Theory of Relativity
-
- ^ Laue, Max von (1911). "Bemerkungen zum Hebelgesetz in der Relativitätstheorie". Physikalische Zeitschrift 12: 1008–1010.
-
- English Wikisource translation: Remarks on the Law of the Lever in the Theory of Relativity
-
- ^ Laue, Max von (1912). "Zur Theorie des Versuches von Trouton und Noble". Annalen der Physik 343 (7): 370–384. Bibcode 1912AnP...343..370L. doi:10.1002/andp.19123430705.
-
- English Wikisource translation: On the Theory of the Experiment of Trouton and Noble
-
- ^ Epstein, P. S. (1911). "Über relativistische Statik". Annalen der Physik 341 (14): 779–795. Bibcode 1911AnP...341..779E. doi:10.1002/andp.19113411404.
-
- English Wikisource translation: Concerning Relativistic Statics
-
- ^ Epstein, P. S. (1927). "Conference on the Michelson-Morley experiment". Contributions from the Mount Wilson Observatory 373: 45–49. Bibcode 1928CMWCI.373...43E. http://articles.adsabs.harvard.edu//full/1928CMWCI.373...43E/0000045.000.html.
Further reading
- History
- Michel Janssen, "A comparison between Lorentz's ether theory and special relativity in the light of the experiments of Trouton and Noble, Ph.D. thesis (1995). Online: TOC, pref., intro-I, 1, 2, intro-II, 3, 4, refs.
- Textbooks
- Tolman, R.C. (1917), "The Right-Angled Lever", The theory of relativity of motion, Berkeley: University of California press, pp. 152-153, http://www.archive.org/details/theoryrelativmot00tolmrich
- Pauli, Wolfgang (1921/1981). "Applications to special cases. Trouton's and Noble's experiment". Theory of Relativity. New York: Dover. pp. 127-130. ISBN 048664152X.
- Panofsky, Wolfgang; Phillips, Melba (1962/2005). Classical electricity and magnetism. Dover. pp. 274, 349. ISBN 0486439240.
- Research papers
- Butler, J. W. (1968). "On the Trouton-Noble Experiment". American Journal of Physics 36 (11): 936–941. Bibcode 1968AmJPh..36..936B. doi:10.1119/1.1974358.
- Aranoff, S. (1969). "Torques and Angular Momentum on a System at Equilibrium in Special Relativity". American Journal of Physics 37 (4): 453–454. Bibcode 1969AmJPh..37..453A. doi:10.1119/1.1975612.
- Furry, W. H. (1969). "Examples of Momentum Distributions in the Electromagnetic Field and in Matter". American Journal of Physics 37 (6): 621–636. Bibcode 1969AmJPh..37..621F. doi:10.1119/1.1975729.
- Newburgh, R. G. (1969). "The relativistic problem of the right-angled lever: The correctness of the Laue solution". Il Nuovo Cimento B 61 (2): 201–209. Bibcode 1969NCimB..61..201N. doi:10.1007/BF02710928.
- Butler, J. W. (1970). "The Lewis-Tolman Lever Paradox". American Journal of Physics 38 (3): 360–368. Bibcode 1970AmJPh..38..360B. doi:10.1119/1.1976326.
- Aranoff, S. (1972). "Equilibrium in special relativity". Il Nuovo Cimento B 10 (1): 155–171. Bibcode 1972NCimB..10..155A. doi:10.1007/BF02911417. http://www.analysis-knowledge.com/Physics/Equilibrium%20in%20Special%20Relativity.pdf.
- Sears, Francis W. (1972). "Another Relativistic Paradox". American Journal of Physics 40 (5): 771–773. Bibcode 1972AmJPh..40..771S. doi:10.1119/1.1986643.
- Aranoff, S. (1973). "More on the Right-Angled Lever at Equilibrium in Special Relativity". American Journal of Physics 41 (9): 1108–1109. Bibcode 1973AmJPh..41.1108A. doi:10.1119/1.1987485.
- Grøn, Ø. (1973). "The asynchronous formulation of relativistic statics and thermodynamics". Il Nuovo Cimento B 17 (1): 141–165. Bibcode 1973NCimB..17..141G. doi:10.1007/BF02906436.
- Nickerson, J. Charles; McAdory, Robert T. (1975). "The Trouton-Noble paradox". American Journal of Physics 43 (7): 615–621. Bibcode 1975AmJPh..43..615N. doi:10.1119/1.9761.
- Grøn, Ø. (1978). "Relativistics statics and F. W. Sears". American Journal of Physics 46 (3): 249–250. Bibcode 1978AmJPh..46..249G. doi:10.1119/1.11164.
- Cavalleri, G.; Grøn, Ø.; Spavieri, G.; Spinelli, G. (1978). "Comment on the article "Right-angle lever paradox" by J. C. Nickerson and R. T. McAdory". American Journal of Physics 46 (1): 108–109. Bibcode 1978AmJPh..46..108C. doi:10.1119/1.11106.
- Holstein, Barry R.; Swift, Arthur R. (1982). "Flexible string in special relativity". American Journal of Physics 50 (10): 887–889. Bibcode 1982AmJPh..50..887H. doi:10.1119/1.13002.
- Aguirregabiria, J. M.; Hernandez, A.; Rivas, M. (1982). "A Lewis-Tolman-like paradox". European Journal of Physics 3 (1): 30–33. Bibcode 1982EJPh....3...30A. doi:10.1088/0143-0807/3/1/008.
- Prokhovnik, S. J.; Kovács, K. P. (1985). "The application of special relativity to the right-angled lever". Foundations of Physics 15 (2): 167–173. Bibcode 1985FoPh...15..167P. doi:10.1007/BF00735288.
- Singal, Ashok K. (1993). "On the "explanation" of the null results of Trouton-Noble experiment". American Journal of Physics 61 (5): 428–433. Bibcode 1993AmJPh..61..428S. doi:10.1119/1.17236.
- Teukolsky, Saul A. (1996). "The explanation of the Trouton-Noble experiment revisited". American Journal of Physics 64 (9): 1104–1109. Bibcode 1996AmJPh..64.1104T. doi:10.1119/1.18329.
- Jefimenko, Oleg D. (1999). "The Trouton-Noble paradox". Journal of Physics A 32 (20): 3755–3762. Bibcode 1999JPhA...32.3755J. doi:10.1088/0305-4470/32/20/308.
- Jackson, J. D. (2004). "Torque or no torque? Simple charged particle motion observed in different inertial frames". American Journal of Physics 72 (12): 1484–1487. Bibcode 2004AmJPh..72.1484J. doi:10.1119/1.1783902.
- Ivezić, Tomislav (2005). "Axiomatic Geometric Formulation of Electromagnetism with Only One Axiom: The Field Equation for the Bivector Field F with an Explanation of the Trouton-Noble Experiment". Foundations of Physics Letters 18 (5): 401–429. arXiv:physics/0412167. Bibcode 2005FoPhL..18..401I. doi:10.1007/s10702-005-7533-7.
- Franklin, Jerrold (2006). "The lack of rotation in the Trouton Noble experiment". European Journal of Physics 27 (5): 1251–1256. arXiv:physics/0603110. Bibcode 2006EJPh...27.1251F. doi:10.1088/0143-0807/27/5/024.
- Ivezić, Tomislav (2006). "Trouton Noble Paradox Revisited". Foundations of Physics 37 (4–5): 747–760. arXiv:physics/0606176. Bibcode 2007FoPh...37..747I. doi:10.1007/s10701-007-9116-x.
- Franklin, Jerrold (2008). "The lack of rotation in a moving right angle lever". European Journal of Physics 29 (6): N55-N58. arXiv:0805.1196. doi:10.1088/0143-0807/29/6/N01.
External links
- Kevin Brown, "Trouton-Noble and The Right-Angle Lever at MathPages.
- Michel Janssen, "The Trouton Experiment and E = mc2," Einstein for Everyone course at UMN (2002).
|
|||||||||||||||||||||||