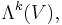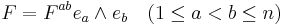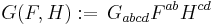Multivector
In multilinear algebra, a multivector or clif is an element of the (graded) exterior algebra on a vector space, 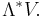 This algebra consists of linear combinations of simple k-vectors (also known as decomposable k-vectors or k-blades)
This algebra consists of linear combinations of simple k-vectors (also known as decomposable k-vectors or k-blades)
"Multivector" may mean either homogeneous elements (all terms of the sum have the same grade or degree k), which are referred to as k-vectors or p-vectors,[1] or may allow sums of terms in different degrees, or may refer specifically to elements of mixed degree.
The k-th exterior power,
is the vector space of formal sums of k-multivectors. The product of a k-multivector and an 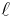 -multivector is a
-multivector is a 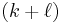 -multivector. So, the direct sum
-multivector. So, the direct sum 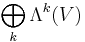 forms an associative algebra, which is closed with respect to the wedge product. This algebra, commonly denoted by
forms an associative algebra, which is closed with respect to the wedge product. This algebra, commonly denoted by 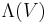 , is called the exterior algebra of V.
, is called the exterior algebra of V.
In differential geometry, a p-vector is the tensor obtained by taking linear combinations of the wedge product of p tangent vectors, for some integer p ≥ 1. It is the dual concept to a p-form.
For p = 2 and 3, these are often called respectively bivectors and trivectors; they are dual to 2-forms and 3-forms.[2][3]
Contents |
Examples
- 0-vectors are scalars;
- 1-vectors are vectors;
- 2-vectors are bivectors;
- (n-1)-vectors are pseudovectors;
- n-vectors are pseudoscalars.
In the presence of a volume form (such as given an inner product and an orientation), pseudovectors and pseudoscalars can be identified with vectors and scalars, which is routine in vector calculus, but without a volume form this cannot be done without a choice.
In the Algebra of physical space (the geometric algebra of Euclidean 3-space, used as a model of 3+1 spacetime), a sum of a scalar and a vector is called a paravector, and represents a point in spacetime (the vector the space, the scalar the time).
Bivectors
A bivector is therefore an element of the antisymmetric tensor product of a tangent space with itself.
In geometric algebra, also, a bivector is a grade 2 element (a 2-vector) resulting from the wedge product of two vectors, and so it is geometrically an oriented area, in the same way a vector is an oriented line segment. If a and b are two vectors, the bivector a ∧ b has
- a norm which is its area, given by
- a direction: the plane where that area lies on, i.e., the plane determined by a and b, as long as they are linearly independent;
- an orientation (out of two), determined by the order in which the originating vectors are multiplied.
Bivectors are connected to pseudovectors, and are used to represent rotations in geometric algebra.
As bivectors are elements of a vector space Λ2V (where V is a finite-dimensional vector space with 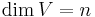 ), it makes sense to define an inner product on this vector space as follows. First, write any element F ∈ Λ2V in terms of a basis (ei ∧ ej)1 ≤ i < j ≤ n of Λ2V as
), it makes sense to define an inner product on this vector space as follows. First, write any element F ∈ Λ2V in terms of a basis (ei ∧ ej)1 ≤ i < j ≤ n of Λ2V as
where the Einstein summation convention is being used.
Now define a map G : Λ2V × Λ2V → R by insisting that
where 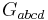 are a set of numbers.
are a set of numbers.
Geometric algebra
In geometric algebra, multivectors are defined to be summations of different-grade k-blades, such as the summation of a scalar, a vector, and a 2-vector.[4] A sum of only n-grade components is called an n-vector,[5] or a homogeneous multivector.[6]
The highest grade element in a space is called the pseudoscalar.
Applications
Bivectors play many important roles in physics, for example, in the classification of electromagnetic fields.
See also
Notes
- ^ Elie Cartan, "The theory of spinors", p. 16, considers only homogeneous vectors, particularly simple ones, referring to them as "multivectors" (collectively) or p-vectors (specifically).
- ^ William M Pezzaglia Jr. (1992). "Clifford algebra derivation of the characteristic hypersurfaces of Maxwell's equations". In Julian Ławrynowicz. Deformations of mathematical structures II. Springer. p. 131 ff. ISBN 0792325761. http://books.google.com/books?id=KfNgBHNUW_cC&pg=PA131. "Hence in 3D we associate the alternate terms of pseudovector for bivector, and pseudoscalar for the trivector"
- ^ Baylis (1994). Theoretical methods in the physical sciences: an introduction to problem solving using Maple V. Birkhäuser. p. 234, see footnote. ISBN 081763715X. http://books.google.com/books?id=pEfMq1sxWVEC&pg=PA234.
- ^ Marcos A. Rodrigues (2000). "§1.2 Geometric algebra: an outline". Invariants for pattern recognition and classification. World Scientific. p. 3 ff. ISBN 9810242786. http://books.google.com/books?id=QbFSt0SlDjIC&pg=PA3.
- ^ R Wareham, J Cameron & J Lasenby (2005). "Applications of conformal geometric algebra in computer vision and graphics". In Hongbo Li, Peter J. Olver, Gerald Sommer. Computer algebra and geometric algebra with applications. Springer. p. 330. ISBN 3540262962. http://books.google.com/books?id=uxofVAQE3LoC&pg=PA330.
- ^ Eduardo Bayro-Corrochano (2004). "Clifford geometric algebra: A promising framework for computer vision, robotics and learning". In Alberto Sanfeliu, José Francisco Martínez Trinidad, Jesús Ariel Carrasco Ochoa. Progress in pattern recognition, image analysis and applications. Springer. p. 25. ISBN 3540235272. http://books.google.com/books?id=gsnXS1xdeekC&pg=PA25.