Trigenus
In low-dimensional topology, the trigenus of a closed 3-manifold is an invariant consisting of an ordered triple 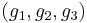 . It is obtained by minimizing the genera of three orientable handle bodies — with no intersection between their interiors— which decompose the manifold as far as the Heegaard genus need only two.
. It is obtained by minimizing the genera of three orientable handle bodies — with no intersection between their interiors— which decompose the manifold as far as the Heegaard genus need only two.
That is, a decomposition  with
with 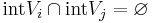 for
for 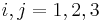 and being
and being 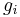 the genus of
the genus of 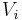 .
.
For orientable spaces,  , where
, where  is
is  's Heegaard genus.
's Heegaard genus.
For non-orientable spaces the 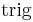 has the form
has the form 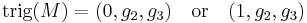 depending on the image of the first Stiefel–Whitney characteristic class
depending on the image of the first Stiefel–Whitney characteristic class 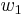 under a Bockstein homomorphism, respectively for
under a Bockstein homomorphism, respectively for 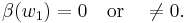
It has been proved that the number 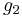 has a relation with the concept of Stiefel–Whitney surface, that is, an orientable surface
has a relation with the concept of Stiefel–Whitney surface, that is, an orientable surface  which is embedded in
which is embedded in  , has minimal genus and represents the first Stiefel–Whitney class under the duality map
, has minimal genus and represents the first Stiefel–Whitney class under the duality map 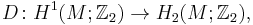 , that is,
, that is, ![Dw_1(M)=[G]](/2012-wikipedia_en_all_nopic_01_2012/I/02c861581f21d34d0c79e6bad5f3ff07.png) . If
. If 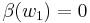 then
then 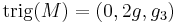 , and if
, and if 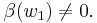 then
then 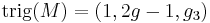 .
.
Theorem
A manifold S is a Stiefel–Whitney surface in M, if and only if S and M−int(N(S)) are orientable .
References
- J.C. Gómez Larrañaga, W. Heil, V.M. Núñez. Stiefel–Whitney surfaces and decompositions of 3-manifolds into handlebodies, Topology Appl. 60 (1994), 267–280.
- J.C. Gómez Larrañaga, W. Heil, V.M. Núñez. Stiefel–Whitney surfaces and the trigenus of non-orientable 3-manifolds, Manuscripta Math. 100 (1999), 405–422.
- "On the trigenus of surface bundles over
 ", 2005, Soc. Mat. Mex. | pdf
", 2005, Soc. Mat. Mex. | pdf