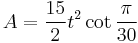Triacontagon
| Regular triacontagon | |
|---|---|
A regular triacontagon |
|
| Type | general type of this shape |
| Edges and vertices | 30 |
| Schläfli symbol | {30} t{15} |
| Coxeter–Dynkin diagrams | |
| Symmetry group | Dihedral (D30) |
| Internal angle (degrees) | 168° |
| Properties | convex, cyclic, equilateral, isogonal, isotoxal |
In geometry, an triacontagon is a thirty-sided polygon. The sum of any triacontagon's interior angles is 5040 degrees.
One interior angle in a regular triacontagon is 168° meaning that one exterior angle would be 12°
The regular triacontagon is a constructible polygon, by an edge-bisection of a regular pentadecagon, and can be seen as a truncated pentadecagon.
Area
The area of a regular triacontangon is (with t = edge length)
Petrie polygons
The regular triacontagon is the Petrie polygon for a number of higher dimensional polytopes with E8 symmetry, shown in orthogonal projections in the E8 Coxeter plane:
(421) |
t1(421) |
t2(421) |
(241) |
t1(241) |
It is also the Petrie polygon for some higher dimensional polytopes with H4 symmetry, shown in orthogonal projections in the H4 Coxeter plane:
120-cell |
Rectified 120-cell |
Rectified 600-cell |
600-cell |
References
|
|||||||||||||||||