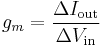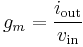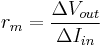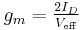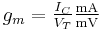Transconductance

Transconductance, also known as mutual conductance, is a property of certain electronic components. Conductance is the reciprocal of resistance; transconductance, meanwhile, is the ratio of the current change at the output port to the voltage change at the input port. It is written as g_m. For direct current, transconductance is defined as follows:

$g_m = {\Delta I_\mathrm{out} \over \Delta V_\mathrm{in}}$

For small signal alternating current, the definition is simpler:

$g_m = {i_\mathrm{out} \over v_\mathrm{in}}$

1 Terminology
- 1.1 Transresistance
2 Devices
3 Amplifiers
4 See also
5 References
6 Further exploration

Terminology

It is a contraction of "transfer conductance". The old unit of conductance, the mho (ohm spelled backwards), was replaced by the SI (International System) unit, the siemens, with the symbol S (1 siemens = 1 ampere per volt).

The origin of the term transistor is a contraction of "transconductance varistor", proposed at Bell Telephone Laboratories, sometimes incorrectly attributed to a contraction of transresistance. See internal BTL opinion poll .

Transresistance

Transresistance, infrequently referred to as mutual resistance, is the dual of transconductance. It is a contraction of "transfer resistance". It refers to the ratio between a change of the voltage at two output points and a related change of current through two input points, and is notated as r_m:

$r_m = {\Delta V_{out} \over \Delta I_{in}}$

The SI unit for transresistance is simply the ohm, as in resistance.

Devices

Vacuum tubes

For vacuum tubes, transconductance is defined as the change in the plate(anode)/cathode current divided by the corresponding change in the grid/cathode voltage, with a constant plate(anode)/cathode voltage. Typical values of g_m for a small-signal vacuum tube are 1 to 10 millisiemens.

Field effect transistors

Similarly, in field effect transistors, and MOSFETs in particular, transconductance is the change in the drain current divided by the small change in the gate/source voltage with a constant drain/source voltage. Typical values of g_m for a small-signal field effect transistor are 1 to 30 millisiemens.

Using the Shichman–Hodges model, the transconductance for the MOSFET can be expressed as (see MOSFET article):

$g_m = \begin{matrix} \frac {2I_D} {V_{\mathrm{eff}}} \end{matrix}\,$

where I_D is the DC drain current at the bias point, and V_eff is the effective voltage, which is the difference between the bias point gate–source voltage and the threshold voltage (i.e., V_eff := V_GS - V_th).^[1]^{:p. 395, Eq. (5.45)} The effective voltage (otherwise known as the overdrive voltage) is customarily chosen at about 70–200 mV for the 65 nm technology node (I_D ≈ 1.13 mA/μm of width) for a g_m of 11–32 mS/μm.^[2]^{:p. 300, Table 9.2}^[3]^{:p. 15, §0127}

Additionally, the transconductance for the junction FET is given by 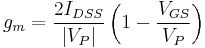$g_m = \frac{{2I_{DSS} }}{{\left| {V_P } \right|}}\left( {1 - \frac{{V_{GS} }}{{V_P }}} \right)$ , where V_P is the pinchoff voltage and I_DSS is the maximum drain current.

Traditionally, the transconductance for the FET and MOSFET as given in the equations above is derived from the transfer equation of each device, using calculus. However, Cartwright ^[4] has shown that this can be done without calculus.

Bipolar transistors

The g_m of bipolar small-signal transistors varies widely, being proportional to the collector current. It has a typical range of 1 to 400 millisiemens. The input voltage change is applied between the base/emitter and the output is the change in collector current flowing between the collector/emitter with a constant collector/emitter voltage.

The transconductance for the bipolar transistor can be expressed as

$g_m = \begin{matrix} \frac {I_C}{V_{T}} \frac{\mathrm{mA}}{\mathrm{mV} } \end{matrix}$

where I_C = DC collector current at the Q-point, and V_T = thermal voltage, typically about 26 mV at room temperature. For a typical current of 10 mA, g_m ≈ 385 mS.

Amplifiers

Transconductance amplifiers

A transconductance amplifier (gm amplifier) puts out a current proportional to its input voltage. In network analysis, the transconductance amplifier is defined as a voltage controlled current source (VCCS) . It is common to see these amplifiers installed in a cascode configuration, which improves the frequency response.

Transresistance amplifiers

Main article: transimpedance amplifier

A transresistance amplifier outputs a voltage proportional to its input current. The transresistance amplifier is often referred to as a transimpedance amplifier, especially by semiconductor manufacturers.

The term for a transresistance amplifier in network analysis is current controlled voltage source (CCVS) .

A basic inverting transresistance amplifier can be built from an operational amplifier and a single resistor. Simply connect the resistor between the output and the inverting input of the operational amplifier and connect the non-inverting input to ground. The output voltage will then be proportional to the input current at the inverting input, decreasing with increasing input current and vice versa.

Specialist chip transresistance (transimpedance) amplifiers are widely used for amplifying the signal current from photo diodes at the receiving end of ultra high speed fibre optic links. The MAX3724 and MAX3725 [1] are examples.

Operational transconductance amplifiers

Many semiconductor manufacturers produce chips (integrated circuits) which can function as transconductance amplifiers. These are frequently described as operational transconductance amplifiers (OTAs) and normally have an input to allow the transconductance to be controlled. Examples are: CA3080 [2], MAX 435 [3], MAX 436 [4], LM13700 [5], OPA860 [6], OPA861 [7].

References

^ Sedra, A.S.; Smith, K.C. (1998), Microelectronic Circuits (Fourth ed.), New York: Oxford University Press, ISBN 0-19-511663-1, http://worldcat.org/isbn/0-19-514251-9
^ Baker, R. Jacob (2010), CMOS Circuit Design, Layout, and Simulation, Third Edition,, New York: Wiley-IEEE, ISBN 978-0-470-88132-3, http://worldcat.org/isbn/978-0-470-88132-3
^ Sansen, W.M.C. (2006), Analog Design Essentials, Dordrecht: Springer, ISBN 0-387-25746-2, http://worldcat.org/isbn/0387257462
^ Cartwright, Kenneth V (Fall 2009), "Derivation of the Exact Transconductance of a FET without Calculus", The Technology Interface Journal 10 (1): 7 pages, http://technologyinterface.nmsu.edu/Fall09/Fall09/011.pdf

Further exploration

Horowitz, Paul & Hill, Winfield (1989), The Art of Electronics, Cambridge University Press, ISBN 0-521-37095-7
Transconductance — SearchSMB.com Definitions
Transconductance in audio amplifiers: article by David Wright of Pure Music [8]