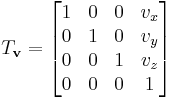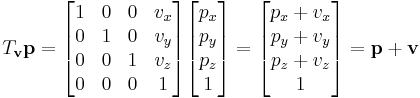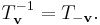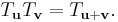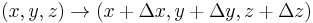Translation (geometry)

In Euclidean geometry, a translation moves every point a constant distance in a specified direction. A translation can be described as a rigid motion: other rigid motions include rotations and reflections. A translation can also be interpreted as the addition of a constant vector to every point, or as shifting the origin of the coordinate system. A translation operator is an operator 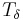T_\mathbf{\delta} such that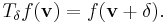 T_\mathbf{\delta} f(\mathbf{v}) = f(\mathbf{v}%2B\mathbf{\delta}).

If v is a fixed vector, then the translation Tv will work as Tv(p) = p + v.

If T is a translation, then the image of a subset A under the function T is the translate of A by T. The translate of A by Tv is often written A + v.

In a Euclidean space, any translation is an isometry. The set of all translations forms the translation group T, which is isomorphic to the space itself, and a normal subgroup of Euclidean group E(n ). The quotient group of E(n ) by T is isomorphic to the orthogonal group O(n ):

E(n ) / T ≅ O(n ).

Contents

Matrix representation

Since a translation is an affine transformation but not a linear transformation, homogeneous coordinates are normally used to represent the translation operator by a matrix and thus to make it linear. Thus we write the 3-dimensional vector w = (wx, wy, wz) using 4 homogeneous coordinates as w = (wx, wy, wz, 1).[1]

To translate an object by a vector v, each homogeneous vector p (written in homogeneous coordinates) would need to be multiplied by this translation matrix:

T_{\mathbf{v}} = \begin{bmatrix} 1 & 0 & 0 & v_x \\ 0 & 1 & 0 & v_y \\ 0 & 0 & 1 & v_z \\ 0 & 0 & 0 & 1 \end{bmatrix}

As shown below, the multiplication will give the expected result:

T_{\mathbf{v}} \mathbf{p} = \begin{bmatrix} 1 & 0 & 0 & v_x \\ 0 & 1 & 0 & v_y\\ 0 & 0 & 1 & v_z\\ 0 & 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} p_x \\ p_y \\ p_z \\ 1 \end{bmatrix} = \begin{bmatrix} p_x %2B v_x \\ p_y %2B v_y \\ p_z %2B v_z \\ 1 \end{bmatrix} = \mathbf{p} %2B \mathbf{v}

The inverse of a translation matrix can be obtained by reversing the direction of the vector:

T^{-1}_{\mathbf{v}} = T_{-\mathbf{v}} . \!

Similarly, the product of translation matrices is given by adding the vectors:

T_{\mathbf{u}}T_{\mathbf{v}} = T_{\mathbf{u}%2B\mathbf{v}} . \!

Because addition of vectors is commutative, multiplication of translation matrices is therefore also commutative (unlike multiplication of arbitrary matrices).

Translations in physics

In physics, translation (Translational motion) is movement that changes the position of an object, as opposed to rotation. For example, according to Whittaker:[2]

If a body is moved from one position to another, and if the lines joining the initial and final points of each of the points of the body are a set of parallel straight lines of length ℓ, so that the orientation of the body in space is unaltered, the displacement is called a translation parallel to the direction of the lines, through a distance ℓ.

— E.T. Whittaker: A Treatise on the Analytical Dynamics of Particles and Rigid Bodies, p. 1

A translation is the operation changing the positions of all points (x, y, z) of an object according to the formula

(x,y,z) \to (x%2B\Delta x,y%2B\Delta y, z%2B\Delta z)

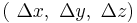where (\ \Delta x,\ \Delta y,\ \Delta z) is the same vector for each point of the object. The translation vector 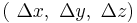(\ \Delta x,\ \Delta y,\ \Delta z) common to all points of the object describes a particular type of displacement of the object, usually called a linear displacement to distinguish it from displacements involving rotation, called angular displacements.

A translation of space (or time) should not be confused with a translation of an object. Such translations have no fixed points.

See also

External links

References

  1. ^ Richard Paul, 1981, Robot manipulators: mathematics, programming, and control : the computer control of robot manipulators, MIT Press, Cambridge, MA
  2. ^ Edmund Taylor Whittaker (1988). A Treatise on the Analytical Dynamics of Particles and Rigid Bodies (Reprint of fourth edition of 1936 with foreword by William McCrea ed.). Cambridge University Press. p. 1. ISBN 0521358833. http://books.google.com/books?id=epH1hCB7N2MC&pg=PA4&dq=rigid+bodies+translation#PPA1,M1.