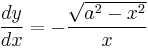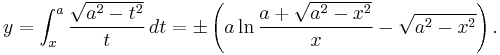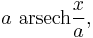Tractrix
Tractrix (from the Latin verb trahere "pull, drag"; plural: tractrices) is the curve along which a small object moves, under the influence of friction, when pulled on a horizontal plane by a piece of thread and a puller that moves at a right angle to the initial line between the object and the puller at an infinitesimal speed. It is therefore a curve of pursuit. It was first introduced by Claude Perrault in 1670, and later studied by Sir Isaac Newton (1676) and Christian Huygens (1692).
Contents |
Mathematical derivation
Suppose the object is placed at (a,0) [or (4,0) in the example shown at right], and the puller in the origin, so a is the length of the pulling thread [4 in the example at right]. Then the puller starts to move along the y axis in the positive direction. At every moment, the thread will be tangent to the curve y = y(x) described by the object, so that it becomes completely determined by the movement of the puller. Mathematically, the movement will be described then by the differential equation
with the initial condition y(a) = 0 whose solution is
The first term of this solution can also be written
where arsech is the inverse hyperbolic secant function.
The negative branch denotes the case where the puller moves in the negative direction from the origin. Both branches belong to the tractrix, meeting at the cusp point (a, 0).
Basis of the tractrix
The essential property of the tractrix is constancy of the distance from a point P on the curve to the intersection of the asymptote and the tangent line at P.
The tractrix might be regarded in a multitude of ways:
- It is the locus of the center of a hyperbolic spiral rolling (without skidding) on a straight line.
- The evolute of the catenary function described by a fully flexible, inelastic, homogeneous string attached to two points and subjected to a gravitational field. It has the equation:
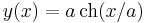
note: the evolvent of the function has a perpendicular tangent to the tangent of the original function for the same x-coordinate considered. - The trajectory determined by the middle of the back axle of a car pulled by a rope at a constant speed and with a constant direction (initially perpendicular to the vehicle).
The function admits a horizontal asymptote. The curve is symmetrical to Oy. The curvature radius is 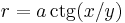
A great implication that the tractrix had was the study of the revolution surface of it around its asymptote: the pseudosphere. Studied by Beltrami in 1868, as a surface of constant negative Gaussian curvature, the pseudosphere is a local model of non-Euclidean geometry. The idea was carried further by Kasner and Newman in their book Mathematics and the Imagination, where they show a toy train dragging a pocket watch to generate the tractrix.
Properties
- Due to the geometrical way it was defined, the tractrix has the property that the segment of its tangent, between the asymptote and the point of tangency, has constant length
 .
. - The arc length of one branch between x = x1 and x = x2 is
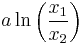
- The area between the tractrix and its asymptote is
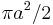 which can be found using integration or Mamikon's theorem.
which can be found using integration or Mamikon's theorem. - The envelope of the normals of the tractrix (that is, the evolute of the tractrix) is the catenary (or chain curve) given by
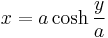 .
. - The surface of revolution created by revolving a tractrix about its asymptote is a pseudosphere.
Practical application
In 1927, P.G.A.H. Voigt patented a horn loudspeaker design based on the assumption that a wave front traveling through the horn is spherical of a constant radius. The idea is to minimize distortion caused by internal reflection of sound within the horn. The resulting shape is the surface of revolution of a tractrix.[1]
Tractrices are also the paths that missiles and torpedoes take as they approach their respective targets.
Drawing machines
- In October–November 1692, Huygens described three tractrice drawing machines.
- In 1693 Leibniz released to the public a machine which, in theory, could integrate any differential equation, the machine was of tractional design.
- In 1706 John Perks built a tractional machine in order to realise the hyperbolic quadrature.
- In 1729 Johann Poleni built a tractional device that enabled logarithmic functions to be drawn.
See also
- Dini's surface
- Hyperbolic functions for tanh, sech, csch, arccosh
- Natural logarithm for ln
- Sign function for sgn
- Trigonometric function for sin, cos, tan, arccot, csc
Notes
References
- Edward Kasner & James Newman (1940) Mathematics and the Imagination, pp 141–3, Simon & Schuster.
- J. Dennis Lawrence (1972). A catalog of special plane curves. Dover Publications. pp. 5, 199. ISBN 0-486-60288-5.