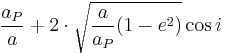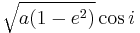Tisserand's parameter
Tisserand's parameter (or Tisserand's invariant) is a combination of orbital elements used in a restricted three-body problem.
Contents |
Definition
For a small body with semimajor axis 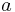 , eccentricity
, eccentricity 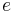 , and inclination
, and inclination 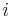 , relative to the orbit of a perturbing larger body with semimajor axis
, relative to the orbit of a perturbing larger body with semimajor axis 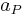 , the parameter is defined as follows:
, the parameter is defined as follows:
The quasi-conservation of Tisserand's parameter is a consequence of Tisserand's relation.
Applications
- TJ, Tisserand’s parameter with respect to Jupiter as perturbing body, is frequently used to distinguish asteroids (typically
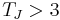 ) from Jupiter-family comets (typically
) from Jupiter-family comets (typically 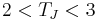 ).
). - The roughly constant value of the parameter before and after the interaction (encounter) is used to determine whether or not an observed orbiting body is the same as a previously observed in Tisserand's Criterion.
- The quasi-conservation of Tisserand's parameter constrains the orbits attainable using gravity assist for outer Solar system exploration.
- TN, Tisserand's parameter with respect to Neptune, has been suggested to distinguish Near Scattered Objects (believed to be affected by Neptune) from Extended Scattered trans-Neptunian objects (e.g. 90377 Sedna).
Related notions
The parameter is derived from one of so called Delaunay standard variables, used to study the perturbed Hamiltonian in 3-body system. Ignoring higher order perturbation terms, the following value is conserved
Consequently, perturbations may lead to the resonance between the orbit inclination and eccentricity, known as Kozai resonance. Near circular, highly inclined orbits can thus become very eccentric (in exchange for lower inclination). As example, such mechanism can produce Sun-grazing comets.1
1Large eccentricity with constant semimajor axis means small perihelion.
See also
- Tisserand's relation for the derivation and the detailed assumptions
External links
- David Jewitt's page on Tisserand's parameter
References
- Murray, Dermot Solar System Dynamics, Cambridge University Press, ISBN 0-521-57597-4
- J. L. Elliot, S. D. Kern, K. B. Clancy, A. A. S. Gulbis, R. L. Millis, M. W. Buie, L. H. Wasserman, E. I. Chiang, A. B. Jordan, D. E. Trilling, and K. J. Meech The Deep Ecliptic Survey: A Search for Kuiper Belt Objects and Centaurs. II. Dynamical Classification, the Kuiper Belt Plane, and the Core Population. The Astronomical Journal, 129 (2006). preprint