Three-phase traffic theory

Three-phase traffic theory is an alternative theory of traffic flow developed by Boris Kerner between 1996 and 2002.^[1]^[2]^[3] It focuses mainly on the explanation of the physics of traffic breakdown and resulting congested traffic on highways. Kerner describes three phases of traffic, while the classical theories based on the fundamental diagram of traffic flow have two phases: free flow and congested traffic. Kerner’s theory divides congested traffic into two distinct phases, synchronized flow and wide moving jam, bringing the total number of phases to three:

Free flow (F)
Synchronized flow (S)
Wide moving jam (J)

The word "wide" is for some reason used even though in fact it is the length of the traffic jam that is being referred to.

A phase is defined as a state in space and time.

1 Free flow (F)
2 Congested traffic
3 Definitions of the phases J and S in congested traffic
4 The fundamental hypothesis of Kerner’s three-phase traffic theory
- 4.1 Steady states of synchronized flow
5 Car following in three-phase traffic theory
6 Traffic breakdown - a F → S phase transition
- 6.1 Spontaneous and induced F → S transitions
- 6.2 Physical explanation of traffic breakdown
7 Range of highway capacities
8 Wide moving jams (J)
- 8.1 Characteristic parameters of wide moving jams
- 8.2 Minimum highway capacity and outflow from wide moving jam
9 Synchronized flow phase (S)
10 S → J phase transition
- 10.1 "Jam without obvious reason" - F→S→J phase transitions
- 10.2 The physics of S → J transition
11 Traffic patterns of S and J
12 Applications of three-phase traffic theory in transportation engineering
13 Criticism of the theory
14 Publications
15 References
16 Notes
17 See also

Free flow (F)

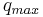In free traffic flow, empirical data show a positive correlation between the flow rate $q$ (in vehicles per unit time) and vehicle density $k$ (in vehicles per unit distance). This relationship stops at the maximum free flow $q_{max}$ with a corresponding critical density 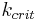$k_{crit}$ . (See Figure 1.)

Congested traffic

Data show a weaker relationship between flow and density in congested conditions. Therefore, Kerner argues that the fundamental diagram, as used in classical traffic theory, cannot adequately describe the complex dynamics of traffic under congested conditions. He instead divides congestion into synchronised flow and wide moving jams.

When the number of vehicles on a road, i.e. the density, becomes too high, the state of the traffic is metastable. This means that when small perturbations occur, the state is still stable; however when larger perturbations occur, the traffic is unstable and moving jams will emerge. Another interpretation of the metastability is the following: the speed at which the downstream front of a congested area moves upstream is higher than the speed at which the upstream front moves upstream (or the latter may actually move downstream). The downstream front will therefore "catch up" with the upstream front, and the moving jam will disappear.

In congested traffic, the vehicle speed is lower than the lowest vehicle speed 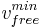$v^{min}_{free}$ encountered in free flow, i.e., the line with the slope of the minimal speed 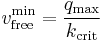$v^\min_\text{free} = \frac{q_\max}{k_\text{crit}}$ in free flow (dotted line in Figure 2) divides the empirical data on the flow-density plane into two regions: on the left side data points of free flow and on the right side data points corresponding to congested traffic.

Definitions of the phases J and S in congested traffic

In Kerner's theory, the phases [J] and [S] in congested traffic are observed outcomes in universal spatial-temporal features of real traffic data. These phases are defined as follows:

The "wide moving jam" phase [J]

A so-called "wide moving jam" moves upstream through any highway bottlenecks. While doing so, the mean velocity of the downstream front 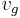$v_g$ is maintained. This is the characteristic feature of the wide moving jam.

The term "wide" has nothing to do with the width across the jam, but actually refers to its length being considerably more than the transition zones at its head and tail.

The "synchronized flow" phase [S]

In "synchronized flow", the downstream front, where the vehicles accelerate to free flow, does not show this characteristic feature of the wide moving jam. Specifically, the downstream front of synchronized flow is often fixed at a bottleneck.

Explanation of the traffic phase definitions based on measured traffic data

Measured data of averaged vehicle speeds (Figure 3 (a)) illustrate the definitions [J] and [S]. There are two spatial-temporal patterns of congested traffic with low vehicle speeds in Figure 3 (a). One pattern propagates upstream with almost constant velocity of the downstream front, moving straight through the freeway bottleneck. According to the definitions, this pattern of congestion belongs to the "wide moving jam" phase. In contrast, the downstream front of the other pattern is fixed at a bottleneck. According to the definitions, this pattern belongs to the "synchronized flow" phase (Figure 3 (a) and (b)).

The fundamental hypothesis of Kerner’s three-phase traffic theory

Steady states of synchronized flow

The fundamental hypothesis of Kerner’s three-phase traffic theory has to do with homogeneous synchronized flow. Homogeneous synchronized flow is a hypothetical state of synchronized flow of identical vehicles and drivers in which all vehicles move with the same time-independent speed and have the same space gaps (a space gap is the distance between one vehicle and the one behind it), i.e., this synchronized flow is homogeneous in time and space. The fundamental hypothesis is that homogeneous synchronized flow can occur anywhere in a two-dimensional region of the flow-density plane (2D-region S in Figure 4(a)). The set of possible free flow states (F) overlaps in vehicle density the set of possible states of homogeneous synchronized flow. The free flow states on a multi-lane road and states of homogeneous synchronized flow are separated by a gap in the flow rate and, therefore, by a gap in the speed at a given density: at each given density the synchronized flow speed is lower than the free flow speed.

In accordance with the fundamental hypothesis of Kerner’s three-phase theory, at a given speed in synchronized flow, the driver can make an arbitrary choice as to the space gap to the preceding vehicle, within the range associated with the 2D region of homogeneous synchronized flow (Figure 4(b)): the driver accepts different space gaps at different times and does not use some one unique gap.

The fundamental hypothesis of Kerner’s three-phase traffic theory is contrary to the hypothesis of earlier traffic flow theories involving the fundamental diagram of traffic flow, which suppose a one-dimensional relationship between vehicle density and flow rate.

Car following in three-phase traffic theory

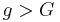In Kerner’s three-phase theory, a vehicle accelerates when the space gap $g$ to the preceding vehicle is greater than a synchronization space gap $G$ , i.e., at $g>G$ (labelled by acceleration in Figure 5); the vehicle decelerates when the gap g is smaller than a safe space gap 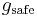$g_{\rm safe}$ , i.e., at 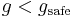$g<g_{\rm safe}$ (labelled by deceleration in Figure 5).

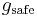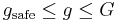If the gap is less than G, the driver tends to adapt his speed to the speed of the preceding vehicle without caring what the precise gap is, so long as this gap is not smaller than the safe space gap $g_{\rm safe}$ (labelled by speed adaptation in Figure 5). Thus the space gap $g$ in car following in the framework of Kerner’s three-phase theory can be any space gap within the space gap range $g_{\rm safe} \leq g \leq G$ .

Traffic breakdown - a F → S phase transition

In measured data, congested traffic most often occurs in the vicinity of highway bottlenecks, e.g., on-ramps, off-ramps, or roadwork. A transition from free flow to congested traffic is known as traffic breakdown. In Kerner’s three-phase traffic theory traffic breakdown is explained by a F → S phase transition. This explanation is supported by available measurements, because in measured traffic data after a traffic breakdown at a bottleneck the downstream front of the congested traffic is fixed at the bottleneck. Therefore, the resulting congested traffic after a traffic breakdown satisfies the definition of the "synchronized flow" phase.

Spontaneous and induced F → S transitions

Kerner notes using empirical data that synchronized flow can form in free flow spontaneously (spontaneous F → S phase transition) or can be externally induced (induced F → S phase transition). A spontaneous F → S phase transition means that the breakdown occurs when there has previously been free flow at the bottleneck as well as both up- and downstream of the bottleneck. This implies that a spontaneous F → S phase transition occurs through the growth of an internal disturbance in free flow in a neighbourhood of a bottleneck. In contrast, an induced F → S phase transition occurs through a disturbance that initially emerged at a different road location downstream from the bottleneck location. Normally, this is in connexion with the upstream propagation of a synchronized flow region or a wide moving jam. An empirical example of an induced breakdown at a bottleneck leading to synchronized flow can be seen in Figure 3: synchronized flow emerges through the upstream propagation of a wide moving jam.

Physical explanation of traffic breakdown

Kerner explains the nature of the F → S phase transitions by an interplay of acceleration while overtaking a slower vehicle and deceleration to the speed of a slower-moving vehicle ahead ("speed adaptation"). Overtaking supports the maintenance of free flow. "Speed adaptation" on the other hand leads to synchronized flow. Speed adaptation will occur if overtaking is not possible. Kerner states that the probability of overtaking is an interrupted function of the vehicle density (Figure 6): at a given vehicle density, the probability of overtaking in free flow is much higher than in synchronized flow.

Range of highway capacities

Maximum and minimum highway capacities

Spontaneous traffic breakdown, i.e., a spontaneous F → S phase transition, may occur in a wide range of flow rates in free flow. Kerner states, based on empirical data, that because of the possibility of spontaneous or induced traffic breakdowns at the same freeway bottleneck there is a range of highway capacities at a bottleneck. This range of freeway capacities is between a minimum capacity 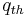$q_{th}$ and a maximum capacity 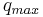$q_{max}$ of free flow (Figure 7).

Highway capacities and metastability of free flow

Even small disturbances in free flow at a bottleneck will lead to a spontaneous F → S phase transition if the flow rate is close to the maximum capacity 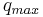$q_{max}$ . (Some models give metastability even at peak flow.^[4]) On the other hand, only very large disturbances in free flow at the bottleneck will lead to a spontaneous F → S phase transition, if the flow rate is close to the minimum capacity 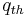$q_{th}$ . The probability of a smaller disturbance in free flow is much higher than that of a larger disturbance. Therefore, the higher the flow rate in free flow at a bottleneck, the higher the probability of the spontaneous F → S phase transition. If the flow rate in free flow is lower than the minimum capacity 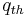$q_{th}$ , there will be no traffic breakdown (no F → S phase transition) at the bottleneck.

The infinite number of highway capacities at a bottleneck can be illustrated by the meta-stability of free flow at flow rates $q$ with

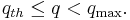
$q_{th} \leq q < q_\max. \,$

Meta-stability of free flow means that for small disturbances free flow remains stable (free flow persists), but with larger disturbances the flow becomes unstable and a F → S phase transition to synchronized flow occurs.

Discussion of capacity definitions

The infinite number of highway capacities at a bottleneck in Kerner’s three-phase traffic theory contradicts fundamentally the classical traffic theories and methods for traffic management and traffic control which at any time assume the existence of a particular highway capacity. In contrast, in Kerner’s three-phase traffic theory at any time there are an infinite number of highway capacities, which are within the above-mentioned flow rate range between the minimum capacity 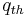$q_{th}$ and maximum capacity 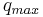$q_{max}$ . 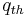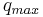The values $q_{th}$ and $q_{max}$ can depend considerably on traffic parameters (the percentage of long vehicles in traffic flow, weather, bottleneck characteristics, etc.).

Wide moving jams (J)

A moving jam will be called "wide" if its length (in direction of the flow) clearly exceeds the lengths of the jam fronts. The average vehicle speed within wide moving jams is much lower than the average speed in free flow. At the downstream front the vehicles accelerate to the free flow speed. At the upstream jam front the vehicles come from free flow or synchronized flow and must reduce their speed. According to the definition [J] the wide moving jam always has the same mean velocity of the downstream front 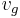$v_{g}$ , even if the jam propagates through other traffic phases or bottlenecks. The flow rate is sharply reduced within a wide moving jam.

Characteristic parameters of wide moving jams

Kerner’s empirical results show that some characteristic features of wide moving jams are independent of the traffic volume and bottleneck features (e.g. where and when the jam formed). However, these characteristic features are dependent on weather conditions, road conditions, vehicle technology, percentage of long vehicles, etc.. The velocity of the downstream front of a wide moving jam 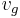$v_{g}$ (in the upstream direction) is a characteristic parameter, as is the flow rate just downstream of the jam 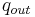$q_{out}$ (with free flow at this location, see Figure 8). This means that many wide moving jams have similar features under similar conditions. These parameters are relatively predictable. The movement of the downstream jam front can be illustrated in the flow-density plane by a line, which is called "Line J" (Line J in Figure 8). The slope of the Line J is the velocity of the downstream jam front $v_{g}$ .

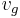Minimum highway capacity and outflow from wide moving jam

Kerner emphasizes that the minimum capacity 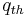$q_{th}$ and the outflow of a wide moving jam 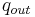$q_{out}$ describe two qualitatively different features of free flow: the minimum capacity 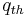$q_{th}$ characterizes an F → S phase transition at a bottleneck, i.e., a traffic breakdown. The outflow of a wide moving jam 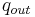$q_{out}$ on the other hand is a condition for the existence of the jam, i.e., the traffic phase J. Depending on traffic parameters like weather, percentage of long vehicles, et cetera, and characteristics of the bottleneck where the F → S phase transition can occur, the minimum capacity 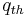$q_{th}$ might be smaller (as in Figure 8), or greater than the jam’s outflow $q_{out}$ .

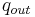Synchronized flow phase (S)

In contrast to wide moving jams, both the flow rate and vehicle speed may vary significantly in the synchronized flow phase. The downstream front of synchronized flow is often spatially fixed (see definition [S]), normally at a bottleneck at a certain road location. The flow rate in this phase could remain similar to the one in free flow, even if the vehicle speeds are sharply reduced.

Because the synchronized flow phase does not have the characteristic features of the wide moving jam phase J, Kerner’s three-phase traffic theory assumes that the hypothetical homogeneous states of synchronized flow cover a two-dimensional region in the flow-density plane (dashed regions in Figure 8).

S → J phase transition

Wide moving jams do not emerge spontaneously in free flow, but they can emerge in regions of synchronized flow. This phase transition is called a S → J phase transition.

"Jam without obvious reason" - F→S→J phase transitions

Therefore, the emergence of a wide moving jam in free flow is observed as a cascade of F → S → J phase transitions: first, a region of synchronized flow emerges in a region of free flow. As explained above, such an F → S phase transition occurs mostly at a bottleneck. Within the synchronized flow phase a further "self-compression” occurs and vehicle density increases while vehicle speed decreases. This self-compression is called "pinch effect". In "pinch" regions of synchronized flow, narrow moving jams emerge. If these narrow moving jams grow, wide moving jams will emerge. Kerner notes that the frequency of the emergence of wide moving jams increases if the density in synchronized flow increases. The wide moving jams propagate further upstream, even if they propagate through regions of synchronized flow or bottlenecks.

The physics of S → J transition

To further illustrate S → J phase transitions, it should be noted that in Kerner’s three-phase traffic theory the Line J divides the homogeneous states of synchronized flow in two (Figure 8). States of homogeneous synchronized flow above Line J are meta-stable. States of homogeneous synchronized flow below Line J are stable states in which no S → J phase transition can occur. Meta-stable homogeneous synchronized flow means that for small disturbances, the traffic state remains stable. However, when larger disturbances occur, synchronized flow becomes unstable, and a S → J phase transition occurs.

Traffic patterns of S and J

Very complex congested patterns can be observed, caused by F → S and S → J phase transitions.

Classification of synchronized flow traffic patterns (SP)

A congestion pattern of synchronized flow (Synchronized Flow Pattern (SP)) with a fixed downstream and a not continuously propagating upstream front is called Localised Synchronized Flow Pattern (LSP).

Frequently the upstream front of a SP propagates upstream. If only the upstream front propagates upstream, the related SP is called Widening Synchronised Flow Pattern (WSP). The downstream front remains at the bottleneck location and the width of the SP increases.

It is possible that both upstream and downstream front propagate upstream. The downstream front is no longer located at the bottleneck. This pattern has been called Moving Synchronised Flow Pattern (MSP).

Catch effect of synchronized flow at a highway bottleneck

The difference between the SP and the wide moving jam becomes visible in that when a WSP or MSP reaches an upstream bottleneck the so-called "catch-effect" can occur. The SP will be caught at the bottleneck and as a result a new congested pattern emerges. A wide moving jam will not be caught at a bottleneck and moves further upstream. In contrast to wide moving jams, the synchronized flow, even if it moves as an MSP, has no characteristic parameters. As an example, the velocity of the downstream front of the MSP might vary significantly and can be different for different MSPs. These features of SP and wide moving jams are consequences of the phase definitions [S] and [J].

General congested traffic pattern (GP)

An often occurring congestion pattern is one that contains both congested phases, [S] and [J]. Such a pattern with [S] and [J] is called General Pattern (GP).

In many freeway infrastructures bottlenecks are very close one to another. A congestion pattern whose synchronized flow covers two or more bottlenecks is called an Expanded Pattern (EP). An EP could contain synchronized flow only (called ESP: Expanded Synchronized Flow Pattern)), but normally wide moving jams form in the synchronized flow. In those cases the EP is called EGP (Expanded General Pattern) (see Figure 9).

Applications of three-phase traffic theory in transportation engineering

One of the applications of Kerner’s three-phase traffic theory is the methods called ASDA/FOTO (Automatische StauDynamikAnalyse (Automatic tracking of wide moving jams) and Forecasting Of Traffic Objects). ASDA/FOTO is a software tool able to process large traffic data volumes quickly and efficiently on freeway networks (see examples from three countries, Figure 10). ASDA/FOTO works in an online traffic management system based on measured traffic data. Recognition, tracking and prediction of [S] and [J] are performed using the features of Kerner’s three-phase traffic theory.

Further applications of the theory are seen in the development of traffic simulation models, a ramp metering system (ANCONA), collective traffic control, traffic assistance and traffic state detection, as described in the books by Kerner.

Criticism of the theory

The theory has been criticized for two primary reasons. First, the theory is almost completely based on measurements on the Bundesautobahn 5 in Germany. It may be that this road has this pattern, but other roads in other countries have other characteristics. Future research must show the validity of the theory on other roads in other countries around the world. Second, it is not clear how the data was interpolated. Kerner uses fixed point measurements (loop detectors), but draws his conclusions on vehicle trajectories, which span the whole length of the road under investigation. These trajectories can only be measured directly if floating car data is used, but as said, only loop detector measurements are used. How the data in between was gathered or interpolated, is not clear.

Other criticisms have been made, such as that the notion of phases has not been well defined and that so-called two-phase models also succeed in simulating the essential features described by Kerner.^[4]

Publications

References

Notes

^ Boris S. Kerner, "Experimental Features of Self-Organization in Traffic Flow", Physical Review Letters, 81, 3797-3400 (1998)
^ Boris S. Kerner, "The physics of traffic", Physics World Magazine 12, 25-30 (August 1999)
^ Boris S. Kerner, "Congested Traffic Flow: Observations and Theory", Transportation Research Record, Vol. 1678, pp. 160-167 (1999)
^ ^a ^b M. Treiber, A. Kesting, D. Helbing, "Three-phase traffic theory and two-phase models with a fundamental diagram in the light of empirical stylized facts". Transportation Research Part B: Methodological 44, 983-1000 (2010). Doi: 10.1016/j.trb.2010.03.004.