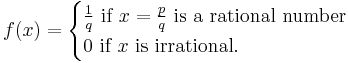Thomae's function
Thomae's function, named after Carl Johannes Thomae, also known as the popcorn function, the raindrop function, the modified Dirichlet function, the ruler function[1], the Riemann function or the Stars over Babylon (by John Horton Conway) is a modification of the Dirichlet function. This real-valued function f(x) is defined as follows:
If x = 0 we take q = 1. It is assumed here that gcd(p, q) = 1 and q > 0 so that the function is well-defined and non-negative.
Contents |
Discontinuities
The popcorn function is perhaps the simplest example of a function with a complicated set of discontinuities: f is continuous at all irrational numbers and discontinuous at all rational numbers.
Informal Proof
Clearly, f is discontinuous at all rational numbers: since the irrationals are dense in the reals, for any rational x, no matter what ε we select, there is an irrational a even nearer to our x where f(a) = 0 (while f(x) is positive). In other words, f can never get "close" to any positive number because its image is dense with zeroes.
To show continuity at the irrationals, assume without loss of generality that our ε is rational (for any irrational ε, we can choose a smaller rational ε and the proof is transitive). Since ε is rational, it can be expressed in lowest terms as a/b. We want to show that f(x) is continuous when x is irrational.
Note that f takes a maximum value of 1 at each whole integer, so we may limit our examination to the space between 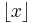 and
and 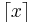 . Since ε has a finite denominator of b, the only values for which f may return a value greater than ε are those with a reduced denominator no larger than b. There exist only a finite number of values between two integers with denominator no larger than b, so these can be exhaustively listed. Setting δ to be smaller than the nearest distance from x to one of these values guarantees every value within δ of x has f(x) < ε.
. Since ε has a finite denominator of b, the only values for which f may return a value greater than ε are those with a reduced denominator no larger than b. There exist only a finite number of values between two integers with denominator no larger than b, so these can be exhaustively listed. Setting δ to be smaller than the nearest distance from x to one of these values guarantees every value within δ of x has f(x) < ε.
Integrability
The Lebesgue criterion for integrability states that a bounded function is Riemann integrable if and only if the set of all discontinuities has measure zero.[2] Since the set of all discontinuities is the rational numbers, and the rational numbers are countable, the set has measure zero. As well, the function is bounded on the interval [0,1], so by the Lebesgue criterion, the function is Riemann integrable on [0,1].
Follow-up
A natural followup question one might ask is if there is a function which is continuous on the rational numbers and discontinuous on the irrational numbers. This turns out to be impossible; the set of discontinuities of any function must be an Fσ set. If such a function existed, then the irrationals would be F-sigma and hence would also be a meager set. It would follow that the real numbers, being a union of the irrationals and the rationals (which is evidently meager), would also be a meager set. This would contradict the Baire category theorem.
A variant of the popcorn function can be used to show that any F-sigma subset of the real numbers can be the set of discontinuities of a function. If  is a countable union of closed sets
is a countable union of closed sets 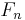 , define
, define
Then a similar argument as for the popcorn function shows that 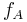 has A as its set of discontinuities.
has A as its set of discontinuities.
See also
- Euclid's orchard – Thomae's function can be interpreted as a perspective drawing of Euclid's orchard
Notes
References
- Robert G. Bartle and Donald R. Sherbert (1999), Introduction to Real Analysis, 3rd Edition (Example 5.1.6 (h)). Wiley. ISBN 978-0471321484
- Spivak, M. Calculus on manifolds. 1965. Perseus Books. ISBN 0-8053-9021-9
- Abbot, Stephen. Understanding Analysis. Berlin: Springer, 2001. ISBN 0-387-95060-5