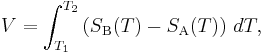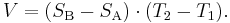Thermoelectric effect
| Thermoelectric effect |
|---|
|
Principles
Thermoelectric effect (Seebeck effect,
Peltier effect, Thomson effect) · Thermopower (Seebeck coefficient) · Ettingshausen effect · Nernst effect |
The thermoelectric effect is the direct conversion of temperature differences to electric voltage and vice-versa. A thermoelectric device creates a voltage when there is a different temperature on each side. Conversely, when a voltage is applied to it, it creates a temperature difference. At the atomic scale, an applied temperature gradient causes charged carriers in the material to diffuse from the hot side to the cold side, similar to a classical gas that expands when heated; hence inducing a thermal current.
This effect can be used to generate electricity, measure temperature or change the temperature of objects. Because the direction of heating and cooling is determined by the polarity of the applied voltage, thermoelectric devices are efficient temperature controllers.
The term "thermoelectric effect" encompasses three separately identified effects: the Seebeck effect, Peltier effect and Thomson effect. Textbooks may refer to it as the Peltier–Seebeck effect. This separation derives from the independent discoveries of French physicist Jean Charles Athanase Peltier and Estonian-German physicist Thomas Johann Seebeck. Joule heating, the heat that is generated whenever a voltage is applied across a resistive material, is related though it is not generally termed a thermoelectric effect. The Peltier–Seebeck and Thomson effects are thermodynamically reversible,[1] whereas Joule heating is not.
Contents |
Seebeck effect
The Seebeck effect is the conversion of temperature differences directly into electricity and is named for German physicist Thomas Johann Seebeck, who, in 1821 discovered that a compass needle would be deflected by a closed loop formed by two metals joined in two places, with a temperature difference between the junctions. This was because the metals responded differently to the temperature difference, creating a current loop and a magnetic field. Seebeck did not recognize there was an electric current involved, so he called the phenomenon the thermomagnetic effect. Danish physicist Hans Christian Ørsted rectified the mistake and coined the term "thermoelectricity". The voltage created by this effect is on the order of several microvolts per kelvin difference. One such combination, copper-constantan, has a Seebeck coefficient of 41 microvolts per kelvin at room temperature.[2]
The voltage V developed can be derived from:
where SA and SB are the thermopowers (Seebeck coefficient) of metals A and B as a function of temperature and T1 and T2 are the temperatures of the two junctions. The Seebeck coefficients are non-linear as a function of temperature, and depend on the conductors' absolute temperature, material, and molecular structure. If the Seebeck coefficients are effectively constant for the measured temperature range, the above formula can be approximated as:
The Seebeck effect is used in the thermocouple to measure a temperature difference; absolute temperature may be found by setting one end to a known temperature. A metal of unknown composition can be classified by its thermoelectric effect if a metallic probe of known composition, kept at a constant temperature, is held in contact with it. Industrial quality control instruments use this as thermoelectric alloy sorting to identify metal alloys. Thermocouples in series form a thermopile, sometimes constructed in order to increase the output voltage, since the voltage induced over each individual couple is small. Thermoelectric generators are used for creating power from heat differentials and exploit this effect.
Thermopower
The thermopower or Seebeck coefficient, represented by S, of a material measures the magnitude of an induced thermoelectric voltage in response to a temperature difference across that material, and the entropy per charge carrier in the material.[3] S has units of V/K, though μV/K is more common. Values in the hundreds of μV/K, regardless of sign, are typical of good thermoelectric materials. The term "thermopower" is a misnomer since it does not measure power, but measures the voltage induced in response to a temperature difference. An applied temperature difference causes charged carriers in the material to diffuse from the hot side to the cold side. Mobile charged carriers migrating to the cold side leave behind their oppositely charged nuclei at the hot side thus giving rise to a thermoelectric voltage. Since a separation of charges creates an electric potential, the buildup of charged carriers onto the cold side eventually ceases at some maximum value since the electric field is at equilibrium. An increase in the temperature difference resumes a buildup of charge carriers on the cold side, leading to an increase in the thermoelectric voltage, and vice versa. The material's temperature and crystal structure influence S; typically metals have small thermopowers because of half-filled bands caused by equal negative and positive charges cancelling each other contributing to the induced thermoelectric voltage. In contrast, semiconductors can be doped with excess electrons or electron holes, causing the magnitude of S to be large. The sign of the thermopower determines which charged carriers dominate the electric transport.
If the temperature difference 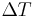 between the two ends of a material is small, then the thermopower of a material is defined approximately[4] as:
between the two ends of a material is small, then the thermopower of a material is defined approximately[4] as:
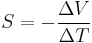
and a thermoelectric voltage of ΔV is seen at the terminals.
This can be written in relation to the electric field  and the temperature gradient
and the temperature gradient 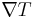 by the approximate[4] equation:
by the approximate[4] equation:
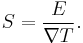
The absolute thermopower of the material of interest is rarely practically measured because electrodes attached to a voltmeter must be placed onto the material in order to measure the thermoelectric voltage, inducing a thermoelectric voltage across one leg of the measurement electrodes. The measured thermopower then includes the thermopower of the material of interest and the material of the measurement electrodes and is written as:
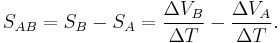
Superconductors have S = 0 since the charged carriers produce no entropy. This allows a direct measurement of the absolute thermopower of the material of interest, since it is the thermopower of the entire thermocouple. In addition, a measurement of the Thomson coefficient  , of a material yields the thermopower through the relation
, of a material yields the thermopower through the relation 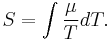
S is an important material parameter that determines the efficiency of a thermoelectric material; a larger induced thermoelectric voltage and a higher S mean a higher efficiency.
Charge-carrier diffusion
The Seebeck effect is caused by two things: charge-carrier diffusion and phonon drag. Charge carriers in the materials will diffuse when one end of a conductor is at a different temperature than the other. Hot carriers diffuse from the hot end to the cold end, since there is a lower density of hot carriers at the cold end of the conductor, and vice versa. If the conductor were left to reach thermodynamic equilibrium, this process would result in heat being distributed evenly throughout the conductor (see heat transfer). The movement of heat (in the form of hot charge carriers) from one end to the other is a heat current and an electric current as charge carriers are moving.
In a system where both ends are kept at a constant temperature difference, there is a constant diffusion of carriers. If the rate of diffusion of hot and cold carriers in opposite directions is equal, there is no net change in charge. The diffusing charges are scattered by impurities, imperfections, and lattice vibrations or phonons. If the scattering is energy dependent, the hot and cold carriers will diffuse at different rates, creating a higher density of carriers at one end of the material and an electrostatic voltage.
This electric field opposes the uneven scattering of carriers, and an equilibrium is reached where the net number of carriers diffusing in one direction is canceled by the net number of carriers moving in the opposite direction. This means the thermopower of a material depends greatly on impurities, imperfections, and structural changes that vary with temperature and electric field; the thermopower of a material is a collection of many different effects.
Early thermocouples were metallic, but many more recently developed thermoelectric devices are made from alternating p-type and n-type semiconductor elements connected by metallic connectors. Semiconductor junctions are common in power generation devices, while metallic junctions are more common in temperature measurement. Charge flows through the n-type element, crosses a metallic interconnect, and passes into the p-type element. If a power source is provided, the thermoelectric device may act as a cooler by the Peltier effect described below. Electrons in the n-type element move opposite the direction of current and holes in the p-type element will move in the direction of current, both removing heat from one side of the device. When a heat source is provided, the thermoelectric device functions as a power generator. The heat source drives electrons in the n-type element toward the cooler region, creating a current through the circuit. Holes in the p-type element then flow in the direction of the current. Therefore, thermal energy is converted into electrical energy.
Phonon drag
Phonons are not always in local thermal equilibrium; they move against the thermal gradient. They lose momentum by interacting with electrons (or other carriers) and imperfections in the crystal. If the phonon-electron interaction is predominant, the phonons will tend to push the electrons to one end of the material, hence losing momentum and contributing to the thermoelectric field. This contribution is most important in the temperature region where phonon-electron scattering is predominant. This happens for
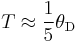
where θD is the Debye temperature. At lower temperatures there are fewer phonons available for drag, and at higher temperatures they tend to lose momentum in phonon-phonon scattering instead of phonon-electron scattering. This region of the thermopower-versus-temperature function is highly variable under a magnetic field.
Peltier effect
The Peltier effect is the presence of heat at an electrified junction of two different metals and is named for French physicist Jean-Charles Peltier, who discovered it in 1834. When a current is made to flow through a junction made of materials A and B, heat is generated at the upper junction at T2, and absorbed at the lower junction at T1. The Peltier heat 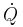 absorbed by the lower junction per unit time is equal to
absorbed by the lower junction per unit time is equal to
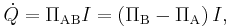
where ΠAB is the Peltier coefficient for the thermocouple composed of materials A and B and ΠA (ΠB) is the Peltier coefficient of material A (B). Π varies with the material's temperature and its specific composition: p-type silicon typically has a positive Peltier coefficient below ~550 K, but n-type silicon is typically negative.
The Peltier coefficients represent how much heat current is carried per unit charge through a given material. Since charge current must be continuous across a junction, the associated heat flow will develop a discontinuity if ΠA and ΠB are different. Depending on the magnitude of the current, heat must accumulate or deplete at the junction due to a non-zero divergence there caused by the carriers attempting to return to the equilibrium that existed before the current was applied by transferring energy from one connector to another. Individual couples can be connected in series to enhance the effect. Thermoelectric heat pumps exploit this phenomenon, as do thermoelectric cooling devices found in refrigerators.
Thomson effect
The Thomson effect was predicted and subsequently observed by Lord Kelvin in 1851. It describes the heating or cooling of a current-carrying conductor with a temperature gradient.
Any current-carrying conductor (except for a superconductor) with a temperature difference between two points either absorbs or emits heat, depending on the material. If a current density J is passed through a homogeneous conductor, the heat production q per unit volume is:
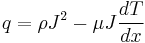
where ρ is the resistivity of the material, dT/dx is the temperature gradient along the wire and μ is the Thomson coefficient. The first term is the Joule heating, which does not change in sign; the second term is the Thomson heating, which follows J changing sign.
In metals such as zinc and copper, whose temperature is directly proportional to their potential, when current moves from the hotter end to the colder end, there is a generation of heat and the positive Thomson effect occurs. Conversely, in metals such as cobalt, nickel, and iron, whose temperature is inversely proportional to their potential, when current moves from the hotter end to the colder end, there is an absorption of heat and the negative Thomson effect occurs.
If the Thomson coefficient of a material is measured over a wide temperature range, it can be integrated using the Thomson relations to determine the absolute values for the Peltier and Seebeck coefficients. This needs to be done only for one material, since the other values can be determined by measuring pairwise Seebeck coefficients in thermocouples containing the reference material and then adding back the absolute thermopower of the reference material.
Lead is commonly stated to have a Thomson coefficient of zero; in fact, it is non-zero, albeit being very small.[5] In contrast, the thermoelectric coefficients of all known superconductors are zero.
Thomson relations
The Thomson coefficient is unique among the three main thermoelectric coefficients because it is the only one directly measurable for individual materials. The Peltier and Seebeck coefficients can only be determined for pairs of materials; hence, no direct methods exist for determining absolute Seebeck or Peltier coefficients for an individual material. In 1854, Lord Kelvin found relationships between the three coefficients, implying that only one could be considered unique.
The first Thomson relation is
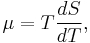
where T is the absolute temperature, μ is the Thomson coefficient and S is the Seebeck coefficient. The second Thomson relation is
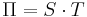
where Π is the Peltier coefficient. It predicted the Thomson effect before it was formalized.
Figure of merit
The figure of merit Z for thermoelectric devices is defined as
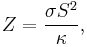
where σ is the electrical conductivity, κ is the thermal conductivity, and S is the Seebeck coefficient. The dimensionless figure of merit ZT is formed by multiplying Z with the average temperature
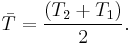
A greater ZT indicates a greater thermodynamic efficiency, subject to certain provisions, particularly that the two materials in the couple have similar Z. ZT is therefore a method for comparing the potential efficiency of devices using different materials. Values of 1 are considered good; values in the 3–4 range are essential for thermoelectrics to compete with mechanical devices in efficiency. To date, the best reported ZT values are in the 2–3 range.[6][7][8] Much of the research in thermoelectric materials has focused on increasing S and reducing κ by manipulating the nanostructure of the materials.
Device efficiency
The efficiency of a thermoelectric device for electricity generation is given by η, defined as
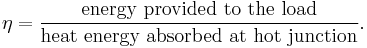
The maximum efficiency ηmax is defined as
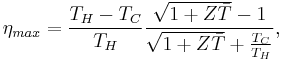
where TH is the temperature at the hot junction and TC is the temperature at the surface being cooled. 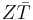 is the modified dimensionless figure of merit, which takes into consideration the thermoelectric capacity of both thermoelectric materials being used in the device and is defined as
is the modified dimensionless figure of merit, which takes into consideration the thermoelectric capacity of both thermoelectric materials being used in the device and is defined as
![Z\bar{T} = {(S_p - S_n)^2 \bar{T} \over [(\rho_n \kappa_n)^{1/2} %2B (\rho_p \kappa_p)^{1/2}]^2}](/2012-wikipedia_en_all_nopic_01_2012/I/1b5a44747889a45f39c5d82b7c89c108.png)
where ρ is the electrical resistivity, 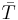 is the average temperature between the hot and cold surfaces and the subscripts n and p denote properties related to the n- and p-type semiconducting thermoelectric materials, respectively. Since thermoelectric devices are heat engines, their efficiency is limited by the Carnot efficiency, hence the TH and TC terms in
is the average temperature between the hot and cold surfaces and the subscripts n and p denote properties related to the n- and p-type semiconducting thermoelectric materials, respectively. Since thermoelectric devices are heat engines, their efficiency is limited by the Carnot efficiency, hence the TH and TC terms in 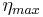 . Regardless, the coefficient of performance of current commercial thermoelectric refrigerators ranges from 0.3 to 0.6, one-sixth the value of traditional vapor-compression refrigerators.[9]
. Regardless, the coefficient of performance of current commercial thermoelectric refrigerators ranges from 0.3 to 0.6, one-sixth the value of traditional vapor-compression refrigerators.[9]
Applications
Seebeck effect
The Seebeck effect is used in the thermoelectric generator, which functions like a heat engine, but is less bulky, has no moving parts, and is typically more expensive and less efficient. These have a use in power plants for converting waste heat into additional power (a form of energy recycling), and in automobiles as automotive thermoelectric generators (ATGs) for increasing fuel efficiency. Space probes often use radioisotope thermoelectric generators with the same mechanism but using radioisotopes to generate the required heat difference.
Peltier effect
The Peltier effect can be used to create a refrigerator which is compact and has no circulating fluid or moving parts; such refrigerators are useful in applications where their advantages out weigh the disadvantage of their very low efficiency
Temperature measurement
Thermocouples and thermopiles are devices that use the Seebeck effect to measure the temperature difference between two objects, one connected to a voltmeter and the other to the probe. The temperature of the voltmeter, and hence that of the material being measured by the probe, can be measured separately using cold junction compensation techniques.
See also
- Heat transfer
- Joule's laws
- Pyroelectricity – the creation of an electric field in a crystal after uniform heating
- Spintronics
- Thermionic emission
- Thermoacoustic refrigeration
- Thermodiffusion
- Thermoelectric cooling
- Thermoelectric generator
- Thermopile
- Thermopower
References
- ^ As the "figure of merit" approaches infinity, the Peltier–Seebeck effect can drive a heat engine or refrigerator at closer and closer to the Carnot efficiency. DiSalvo, "Thermoelectric Cooling and Power Generation", Science 1999. Any device that works at the Carnot efficiency is thermodynamically reversible, a consequence of classical thermodynamics.
- ^ http://www.bnl.gov/magnets/staff/gupta/cryogenic-data-handbook/Section13.pdf
- ^ Rockwood, Alan L. (1984). "Relationship of thermoelectricity to electronic entropy". Phys. Rev. A 30 (5): 2843–4. Bibcode 1984PhRvA..30.2843R. doi:10.1103/PhysRevA.30.2843. http://link.aps.org/doi/10.1103/PhysRevA.30.2843
- ^ a b Strictly speaking, these two expressions for the Seebeck coefficient are only approximate: The numerator of the first equation should be the difference in (electrochemical potential divided by -e), not electric potential, and likewise the second equation should have the gradient of electrochemical potential divided by e rather than the electric field. The chemical potential is relatively constant as a function of temperature, so using electric potential alone is in these cases a very good approximation. Taylor, 1973. Although many textbooks use the approximate definition, a few give the exact expression; examples are Physics of transition metal oxides by Sadamichi Maekawa, page 323 and Thermoelectrics: Basic Principles and New Materials Developments by Nolas et al., page 38.
- ^ Roberts, R.B. (1977). "Absolute scale of thermoelectricity". Nature 265 (5591): 226–7. Bibcode 1977Natur.265..226R. doi:10.1038/265226a0
- ^ Katie Walter (May 2007). "A Quantum contribution to Technology". Lawrence Livermore National Laboratory. http://www.llnl.gov/str/May07/Williamson.html.
- ^ R. Venkatasubramanian, E. Siivola, T. Colpitts, and B. O’Quinn, Nature 413, 597 2001.
- ^ T. C. Harman, M. P. Walsh, B. E. Laforge, and G. W. Turner, J. Electron. Mater. 34, L19 2005
- ^ Solar refrigeration options – a state-of-the-art review. D.S. Kim, C.A. Infante Ferreira. 2008, International Journal of Refrigeration, pp. 3–15. DOI web link
- Besançon, Robert M. (1985). The Encyclopedia of Physics, Third Edition. Van Nostrand Reinhold Company. ISBN 0-442-25778-3.
- Rowe, D. M., ed (2006). Thermoelectrics Handbook:Macro to Nano. Taylor & Francis. ISBN 0-8493-2264-2.
- Ioffe, A.F. (1957). Semiconductor Thermoelements and Thermoelectric Cooling. Infosearch Limited. ISBN 0-8508-6039-3.
- Thomson, William (1851). "On a mechanical theory of thermoelectric currents". Proc.Roy.Soc.Edinburgh: 91–98.
External links
- Thomson Effect – Interactive Java Tutorial National High Magnetic Field Laboratory
- International Thermoelectric Society
- Thermoelectric News
- General
- Explanation of carrier diffusion and phonon drag components of thermopower
- Good explanation of thermo-electric cooler design
- BSST Technical Papers on thermoelectric devices
- A brief explanation
- An introduction to thermoelectric coolers
- The origin of the thermoelectric potential
- The 8th European Conference on Thermoelectrics, ECT 2010, to be held Sept. 22–24, 2010 in Como, Italy, organized by the Lecco unit of the Institute of Energetics and Interphases (IENI) of the Italian National research Council (CNR)
- A news article on the increases in thermal diode efficiency
- A fan for putting on top of stoves and other hot items, powered by the Peltier-Seebeck effect.
- Generating useful voltages (and powering radio transmitters) from Peltier devices
|
||||||||||||||