Theory of tides
The theory of tides is the application of continuum mechanics to interpret and predict the tidal deformations of planetary and satellite bodies and their atmospheres and oceans, under the gravitational loading of another astronomical body or bodies. It commonly refers to the fluid dynamic motions for the Earth's oceans.
Contents |
Origin of theory
In 1616, Galileo Galilei wrote Discourse on the Tides (in Italian: Discorso del flusso e reflusso del mare),[1] a paper in which he tried to explain the occurrence of the tides as the result of the Earth's rotation around the Sun. However, Galileo's theory was, in the later Newtonian terms, an error.[1] Later analysis over the centuries had led to the current tidal physics.
Tidal physics
Tidal forcing
The forces discussed here apply to body (Earth tides), oceanic and atmospheric tides. Atmospheric tides on Earth, however, tend to be dominated by forcing due to solar heating.
On the planet (or satellite) experiencing tidal motion consider a point at latitude  and longitude
and longitude  at distance
at distance  from the center of mass, then this point can be written in cartesian coordinates as
from the center of mass, then this point can be written in cartesian coordinates as 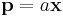 where
where
Let  be the declination and
be the declination and  be the right ascension of the deforming body, the Moon for example, then the vector direction is
be the right ascension of the deforming body, the Moon for example, then the vector direction is
and 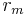 be the orbital distance between the center of masses and
be the orbital distance between the center of masses and 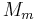 the mass of the body. Then the force on the point is
the mass of the body. Then the force on the point is
where 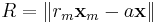
For a circular orbit the angular momentum  centripetal acceleration balances gravity at the planetary center of mass
centripetal acceleration balances gravity at the planetary center of mass
where 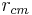 is the distance between the center of mass for the orbit and planet and
is the distance between the center of mass for the orbit and planet and  is the planetary mass. Consider the point in the reference fixed without rotation, but translating at a fixed translation with respect to the center of mass of the planet. The body's centripetal force acts on the point so that the total force is
is the planetary mass. Consider the point in the reference fixed without rotation, but translating at a fixed translation with respect to the center of mass of the planet. The body's centripetal force acts on the point so that the total force is
Substituting for center of mass acceleration, and reordering
In ocean tidal forcing, the radial force is not significant, the next step is to rewrite the 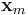 coefficient. Let
coefficient. Let 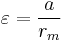 then
then
where 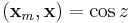 is the inner product determining the angle z of the deforming body or Moon from the zenith. This means that
is the inner product determining the angle z of the deforming body or Moon from the zenith. This means that
if ε is small. If particle is on the surface of the planet then the local gravity is 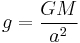 and set
and set 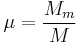 .
.
which is a small fraction of  . Note also that force is attractive toward the Moon when the
. Note also that force is attractive toward the Moon when the 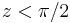 and repulsive when
and repulsive when 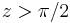 .
.
This can also be used to derive a tidal potential.
Laplace's tidal equations
in 1776, Pierre-Simon Laplace formulated a single set of linear partial differential equations, for tidal flow described as a barotropic two-dimensional sheet flow. Coriolis effects are introduced as well as lateral forcing by gravity. Laplace obtained these equations by simplifying the fluid dynamic equations. But they can also be derived from energy integrals via Lagrange's equation.
For a fluid sheet of average thickness D, the vertical tidal elevation ς, as well as the horizontal velocity components u and v (in the latitude φ and longitude λ directions, respectively) satisfy Laplace's tidal equations[2][3]:
where Ω is the angular frequency of the planet's rotation, g is the planet's gravitational acceleration at the mean ocean surface, and U is the external gravitational tidal-forcing potential.
William Thomson (Lord Kelvin) rewrote Laplace's momentum terms using the curl to find an equation for vorticity. Under certain conditions this can be further rewritten as a conservation of vorticity.
Tidal analysis and prediction
Harmonic analysis
Laplace's improvements in theory were substantial, but they still left prediction in an approximate state. This position changed in the 1860s when the local circumstances of tidal phenomena were more fully brought into account by William Thomson's application of Fourier analysis to the tidal motions. Thomson's work in this field was then further developed and extended by George Darwin: Darwin's work was based on the lunar theory current in his time. His symbols for the tidal harmonic constituents are still used. Darwin's harmonic developments of the tide-generating forces were later brought up to date with modern developments by A T Doodson whose development of the tide generating potential (TGP) in harmonic form was carried out and published in 1921:[4] Doodson distinguished 388 tidal frequencies.[5] Doodson's analysis of 1921 was based on the then-latest lunar theory of E W Brown.[6]
Doodson devised a practical system for specifying the different harmonic components of the tide-generating potential, the Doodson Numbers, a system still in use.[7]
Since the mid-twentieth century further analysis has generated many more terms than Doodson's 388. About 62 constituents are of sufficient size to be considered for possible use in marine tide prediction, but sometimes many less even than that can predict tides to useful accuracy. The calculations of tide predictions using the harmonic constituents are laborious, and from the 1870s to about the 1960s they were carried out using a mechanical tide-predicting machine, a special-purpose form of analog computer now superseded in this work by digital electronic computers that can be programmed to carry out the same computations.
Tidal constituents
Tidal constituents combine to give an endlessly-varying aggregate because of their different and incommensurable frequencies: the effect is visualized in an animation of the American Mathematical Society illustrating the way in which the components used to be mechanically combined in the tide-predicting machine. Amplitudes of tidal constituents are given below for the following example locations:
- ME Eastport,
- MS Biloxi,
- PR San Juan,
- AK Kodiak,
- CA San Francisco, and
- HI Hilo.
Higher harmonics |
Darwin |
Period |
Phase |
Doodson coefs |
Doodson |
Amplitude at example location (cm) |
NOAA |
||||||||
|
Species |
Symbol |
(hr) |
rate(°/hr) |
n1 (L) | n2 (m) | n3 (y) | n4 (mp) |
number |
ME |
MS |
PR |
AK |
CA |
HI |
order |
| Shallow water overtides of principal lunar | M4 | 6.210300601 | 57.9682084 | 4 | 455.555 | 6.0 | 0.6 | 0.9 | 2.3 | 5 | |||||
| Shallow water overtides of principal lunar | M6 | 4.140200401 | 86.9523127 | 6 | 655.555 | 5.1 | 0.1 | 1.0 | 7 | ||||||
| Shallow water terdiurnal | MK3 | 8.177140247 | 44.0251729 | 3 | 1 | 365.555 | 0.5 | 1.9 | 8 | ||||||
| Shallow water overtides of principal solar | S4 | 6 | 60 | 4 | 4 | -4 | 491.555 | 0.1 | 9 | ||||||
| Shallow water quarter diurnal | MN4 | 6.269173724 | 57.4238337 | 4 | -1 | 1 | 445.655 | 2.3 | 0.3 | 0.9 | 10 | ||||
| Shallow water overtides of principal solar | S6 | 4 | 90 | 6 | 6 | -6 | * | 0.1 | 12 | ||||||
| Lunar terdiurnal | M3 | 8.280400802 | 43.4761563 | 3 | 355.555 | 0.5 | 32 | ||||||||
| Shallow water terdiurnal | 2"MK3 | 8.38630265 | 42.9271398 | 3 | -1 | 345.555 | 0.5 | 0.5 | 1.4 | 34 | |||||
| Shallow water eighth diurnal | M8 | 3.105150301 | 115.9364166 | 8 | 855.555 | 0.5 | 0.1 | 36 | |||||||
| Shallow water quarter diurnal | MS4 | 6.103339275 | 58.9841042 | 4 | 2 | -2 | 473.555 | 1.8 | 0.6 | 1.0 | 37 | ||||
Semi-diurnal |
Darwin |
Period |
Phase |
Doodson coefs |
Doodson |
Amplitude at example location (cm) |
NOAA |
||||||||
| Species |
Symbol |
(hr) |
(°/hr) |
n1 (L) | n2 (m) | n3 (y) | n4 (mp) |
number |
ME |
MS |
PR |
AK |
CA |
HI |
order |
| Principal lunar semidiurnal | M2 | 12.4206012 | 28.9841042 | 2 | 255.555 | 268.7 | 3.9 | 15.9 | 97.3 | 58.0 | 23.0 | 1 | |||
| Principal solar semidiurnal | S2 | 12 | 30 | 2 | 2 | -2 | 273.555 | 42.0 | 3.3 | 2.1 | 32.5 | 13.7 | 9.2 | 2 | |
| Larger lunar elliptic semidiurnal | N2 | 12.65834751 | 28.4397295 | 2 | -1 | 1 | 245.655 | 54.3 | 1.1 | 3.7 | 20.1 | 12.3 | 4.4 | 3 | |
| Larger lunar evectional | ν2 | 12.62600509 | 28.5125831 | 2 | -1 | 2 | -1 | 247.455 | 12.6 | 0.2 | 0.8 | 3.9 | 2.6 | 0.9 | 11 |
| Variational | MU2 | 12.8717576 | 27.9682084 | 2 | -2 | 2 | 237.555 | 2.0 | 0.1 | 0.5 | 2.2 | 0.7 | 0.8 | 13 | |
| Lunar elliptical semidiurnal second-order | 2"N2 | 12.90537297 | 27.8953548 | 2 | -2 | 2 | 235.755 | 6.5 | 0.1 | 0.5 | 2.4 | 1.4 | 0.6 | 14 | |
| Smaller lunar evectional | λ2 | 12.22177348 | 29.4556253 | 2 | 1 | -2 | 1 | 263.655 | 5.3 | 0.1 | 0.7 | 0.6 | 0.2 | 16 | |
| Larger solar elliptic | T2 | 12.01644934 | 29.9589333 | 2 | 2 | -3 | 272.555 | 3.7 | 0.2 | 0.1 | 1.9 | 0.9 | 0.6 | 27 | |
| Smaller solar elliptic | R2 | 11.98359564 | 30.0410667 | 2 | 2 | -1 | 274.555 | 0.9 | 0.2 | 0.1 | 0.1 | 28 | |||
| Shallow water semidiurnal | 2SM2 | 11.60695157 | 31.0158958 | 2 | 4 | -4 | 291.555 | 0.5 | 31 | ||||||
| Smaller lunar elliptic semidiurnal | L2 | 12.19162085 | 29.5284789 | 2 | 1 | -1 | 265.455 | 13.5 | 0.1 | 0.5 | 2.4 | 1.6 | 0.5 | 33 | |
| Lunisolar semidiurnal | K2 | 11.96723606 | 30.0821373 | 2 | 2 | 275.555 | 11.6 | 0.9 | 0.6 | 9.0 | 4.0 | 2.8 | 35 | ||
Diurnal |
Darwin |
Period |
Phase |
Doodson coefs |
Doodson |
Amplitude at example location (cm) |
NOAA |
||||||||
| Species |
Symbol |
(hr) |
(°/hr) |
n1 (L) | n2 (m) | n3 (y) | n4 (mp) |
number |
ME |
MS |
PR |
AK |
CA |
HI |
order |
| Lunar diurnal | K1 | 23.93447213 | 15.0410686 | 1 | 1 | 165.555 | 15.6 | 16.2 | 9.0 | 39.8 | 36.8 | 16.7 | '4 | ||
| Lunar diurnal | O1 | 25.81933871 | 13.9430356 | 1 | -1 | 145.555 | 11.9 | 16.9 | 7.7 | 25.9 | 23.0 | 9.2 | 6 | ||
| Lunar diurnal | OO1 | 22.30608083 | 16.1391017 | 1 | 3 | 185.555 | 0.5 | 0.7 | 0.4 | 1.2 | 1.1 | 0.7 | 15 | ||
| Solar diurnal | S1 | 24 | 15 | 1 | 1 | -1 | 164.555 | 1.0 | 0.5 | 1.2 | 0.7 | 0.3 | 17 | ||
| Smaller lunar elliptic diurnal | M1 | 24.84120241 | 14.4920521 | 1 | 155.555 | 0.6 | 1.2 | 0.5 | 1.4 | 1.1 | 0.5 | 18 | |||
| Smaller lunar elliptic diurnal | J1 | 23.09848146 | 15.5854433 | 1 | 2 | -1 | 175.455 | 0.9 | 1.3 | 0.6 | 2.3 | 1.9 | 1.1 | 19 | |
| Larger lunar evectional diurnal | ρ | 26.72305326 | 13.4715145 | 1 | -2 | 2 | -1 | 137.455 | 0.3 | 0.6 | 0.3 | 0.9 | 0.9 | 0.3 | 25 |
| Larger lunar elliptic diurnal | Q1 | 26.868350 | 13.3986609 | 1 | -2 | 1 | 135.655 | 2.0 | 3.3 | 1.4 | 4.7 | 4.0 | 1.6 | 26 | |
| Larger elliptic diurnal | 2Q1 | 28.00621204 | 12.8542862 | 1 | -3 | 2 | 125.755 | 0.3 | 0.4 | 0.2 | 0.7 | 0.4 | 0.2 | 29 | |
| Solar diurnal | P1 | 24.06588766 | 14.9589314 | 1 | 1 | -2 | 163.555 | 5.2 | 5.4 | 2.9 | 12.6 | 11.6 | 5.1 | 30 | |
Long period |
Darwin |
Period |
Phase |
Doodson coefs |
Doodson |
Amplitude at example location (cm) |
NOAA |
||||||||
| Species |
Symbol |
(hr) |
(°/hr) |
n1 (L) | n2 (m) | n3 (y) | n4 (mp) |
number |
ME |
MS |
PR |
AK |
CA |
HI |
order |
| Lunar monthly | Mm | 661.3111655 | 0.5443747 | 0 | 1 | -1 | 65.455 | 0.7 | 1.9 | 20 | |||||
| Solar semiannual | Ssa | 4383.076325 | 0.0821373 | 0 | 2 | 57.555 | 1.6 | 2.1 | 1.5 | 3.9 | 21 | ||||
| Solar annual | Sa | 8766.15265 | 0.0410686 | 0 | 1 | 56.555 | 5.5 | 7.8 | 3.8 | 4.3 | 22 | ||||
| Lunisolar synodic fortnightly | Msf | 354.3670666 | 1.0158958 | 0 | 2 | -2 | 73.555 | 1.5 | 23 | ||||||
| Lunisolar fortnightly | Mf | 327.8599387 | 1.0980331 | 0 | 2 | 75.555 | 1.4 | 2.0 | 0.7 | 24 | |||||
References
- ^ a b Rice University - Galileo's Theory of the Tides - by Rossella Gigli, retrieved 10 March 2010
- ^ http://kiwi.atmos.colostate.edu/group/dave/pdf/LTE.frame.pdf
- ^ http://siam.org/pdf/news/621.pdf
- ^ A T Doodson (1921), "The Harmonic Development of the Tide-Generating Potential", Proceedings of the Royal Society of London. Series A, Vol. 100, No. 704 (Dec. 1, 1921), pp. 305-329.
- ^ S Casotto, F Biscani, "A fully analytical approach to the harmonic development of the tide-generating potential accounting for precession, nutation, and perturbations due to figure and planetary terms", AAS Division on Dynamical Astronomy, April 2004, vol.36(2), 67.
- ^ D E Cartwright, "Tides: a scientific history", Cambridge University Press 2001, at pages 163-4.
- ^ See e.g. T D Moyer (2003), "Formulation for observed and computed values of Deep Space Network data types for navigation", vol.3 in Deep-space communications and navigation series, Wiley (2003), e.g. at pp.126-8.
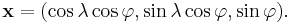
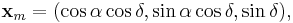
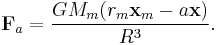
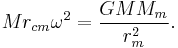
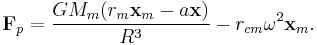
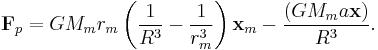
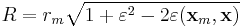
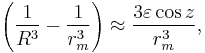
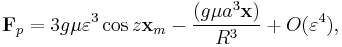
![\begin{align}
\frac{\partial \zeta}{\partial t}
&%2B \frac{1}{a \cos( \varphi )} \left[
\frac{\partial}{\partial \lambda} (uD)
%2B \frac{\partial}{\partial \varphi} \left(vD \cos( \varphi )\right)
\right]
= 0,
\\[2ex]
\frac{\partial u}{\partial t}
&- v \left( 2 \Omega \sin( \varphi ) \right)
%2B \frac{1}{a \cos( \varphi )} \frac{\partial}{\partial \lambda} \left( g \zeta %2B U \right)
=0
\qquad \text{and} \\[2ex]
\frac{\partial v}{\partial t}
&%2B u \left( 2 \Omega \sin( \varphi ) \right)
%2B \frac{1}{a} \frac{\partial}{\partial \varphi} \left( g \zeta %2B U \right)
=0,
\end{align}](/2012-wikipedia_en_all_nopic_01_2012/I/da3612f7bbfcc628306d42811b1e8561.png)