Themistocles M. Rassias
| Themistocles M. Rassias | |
|---|---|
Rassias around 2005
|
|
| Born | April 2, 1951 Pellana, Peloponnese, Greece |
| Residence | Greece |
| Nationality | Greek |
| Fields | Mathematics |
| Institutions | National Technical University of Athens |
| Alma mater | University of California, Berkeley (Ph.D.) |
| Doctoral advisor | Stephen Smale |
| Known for | Hyers–Ulam–Rassias stability[1][2] Aleksandrov–Rassias problem[3][4] |
| Influences | Stephen Smale, S. M. Ulam |
| Notable awards | Doctor Honoris Causa, University of Alba Iulia,[5] Romania (2008) Honorary Doctorate, University of Nis,[6] Serbia (2010) |
Themistocles M. Rassias (Greek: Θεμιστοκλής Μ. Ρασσιάς; born on April 2, 1951; in Pellana, Peloponnese, Greece) is a Greek mathematician, and a professor at the National Technical University of Athens (Eθνικό Μετσόβιο Πολυτεχνείο), Greece. He has published more than 220 papers, 6 research books and 30 edited volumes in research Mathematics as well as 4 textbooks in Mathematics (in Greek) for university students. His research work has received a large number of citations by several mathematicians. He serves as a member of the Editorial Board of several mathematical journals.
Contents |
Education
He received his Ph.D. in Mathematics from the University of California at Berkeley in June 1976. Professor Stephen Smale and Professor Shiing-Shen Chern have been his thesis and academic advisors, respectively.
Research
His work extends over several fields of Mathematical Analysis. It includes Global Analysis, Analysis on Manifolds, Calculus of Variations, Nonlinear Functional Analysis, Approximation Theory, Functional Equations, Inequalities, Metric Geometry and their Applications.
He has contributed a number of results in the stability of minimal submanifolds, in the solution of Ulam's Problem for approximate homomorphisms in Banach spaces, in the theory of isometric mappings in metric spaces and in Complex analysis (Poincare's inequality and harmonic mappings).
Mathematical Terminology
Some of his research work has been established with the scientific terminology:
(i) Hyers–Ulam–Rassias stability [1] [2] of functional equations. (ii) The Aleksandrov–Rassias problem[3][4] for isometric mappings.[7]
Awards and honors
He has received a number of honors and awards including:
- 1977–1978 and 1978–1979, Membership offer from the School of Mathematics of the Institute for Advanced Study in Princeton, that he could not accept for family reasons.
- 1980, Research Associate at the Department of Mathematics of Harvard University, invited by Raoul Bott.
- 1980, Visiting Research Professor at the Department of Mathematics of the Massachusetts Institute of Technology, invited by F. P. Peterson.
- 1985–1986, 1986–1987, Teacher of the Year.
- 1987, Accademico Ordinario of the Accademia Tiberina, Roma.
- 1989–1990, 1990–1991, 1991–1992, Outstanding Faculty Member, University of La Verne, California (Athens Campus).
- 1991, Fellow of the Royal Astronomical Society of London.
- 2003, A volume entitled Stability of Functional Equations of Ulam-Hyers-Rassias Type was dedicated to the 25 years since the publication of Th. M. Rassias' Theorem, edited by S. Czerwik, Hadronic Press Inc., Florida.
- 2007, A special volume of the Banach Journal of Math. Analysis (Vol. 1, Issues 1 & 2) was dedicated to the 30th Anniversary of Th. M. Rassias' Stability Theorem.
- 2008, Doctor Honoris Causa (DHC), University of Alba Iulia (Romania).
- 2009, Α special issue of the Journal Nonlinear Functional Analysis and Applications (Vol.14, No.5) was dedicated to the 30th Anniversary of Th. M. Rassias' Stability Theorem.
- 2010, Ulam Prize in Mathematics.
- 2010, Honorary Doctorate, University of Nis (Serbia).
- 2011, Α special issue of the Journal Nonlinear Sciences and Applications is dedicated to the 60th Anniversary of Th. M. Rassias' birth.
- 2011, A volume entitled Nonlinear Analysis: Stability, Approximation and Inequalities is dedicated to the 60th Anniversary of Th. M. Rassias' birth. (To be published by Springer, New York, 2011).
See also
- Hyers-Ulam-Rassias stability, in: Encyclopaedia of Mathematics, Supplement III Hazewinkel, M. (ed.), Kluwer (2001) ISBN 1-4020-0198-3, pp. 194–196.
- Ulam-Hyers-Rassias Stability of Functional Equations, in: S. Czerwik, Functional Equations and Inequalities in Several Variables (Part II, pp. 129–260).
References
- ^ a b Jung, Soon-Mo (2011). Hyers–Ulam–Rassias Stability of Functional Equations in Nonlinear Analysis. New York, USA: Springer. pp. 377. ISBN 978-1-4419-9636-7.
- ^ a b "Hyers-Ulam-Rassias stability". http://www.sciencedirect.com/science?_ob=MImg&_imagekey=B6WK2-45NSHPB-8F-1&_cdi=6894&_user=83473&_pii=S0022247X8471211X&_origin=browse&_zone=rslt_list_item&_coverDate=06%2F15%2F1994&_sk=998159996&wchp=dGLbVtb-zSkWA&md5=a1b422e03169eb492a9561f8b9877a0c&ie=/sdarticle.pdf.
- ^ a b "On the Aleksandrov-Rassias problem for isometric mappings". http://www.ams.org/mathscinet/pdf/2042566.pdf?pg1=IID&s1=342623&vfpref=html&r=30.
- ^ a b "On the Aleksandrov-Rassias problem and the geometric invariance in Hilbert spaces". http://www.ams.org/mathscinet/pdf/2101186.pdf?pg1=IID&s1=342623&vfpref=html&r=27.
- ^ "University of Alba Iulia". http://en.wikipedia.org/wiki/1_Decembrie_1918_University,_Alba_Iulia.
- ^ "University of Nis". http://www.ni.ac.rs/en/.
- ^ An interview with Themistocles M. Rassias
- J.-R. Lee and D.-Y. Shin, On the Cauchy-Rassias stability of a generalized additive functional equation, J. Math. Anal. Appl. 339(1)(2008), 372–383.
- A. Najati, Cauchy-Rassias stability of homomorphisms associated to a Pexiderized Cauchy-Jensen type functional equation, J. Math. Inequal. 3(2)(2009), 257-265.
- C. Baak, H.- Y. Chu and M. S. Moslehian, On the Cauchy-Rassias inequality and linear n–inner product preserving mappings, Math. Inequal. Appl. 9(3)(2006), 453–464.
- C.-G. Park, Homomorphisms between Lie JC*- algebras and Cauchy – Rassias stability of Lie JC*-algebra derivations, J. Lie Theory, 15(2005), 393–414.
- M. Craioveanu, M. Puta and Th.M. Rassias, Old and New Aspects in Spectral Geometry, Kluwer Academic Publishers, Dordrecht, Boston, London, 2001.
- P. Enflo and M.S. Moslehian, An interview with Themistocles M. Rassias, Banach J. Math. Anal., 1 (2007), no. 2, 252-260.
- V. A. Faizev, Th. M. Rassias and P. K. Sahoo, The space of
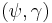-additive mappings on semigroups, Transactions of the American Mathematical Society 354(11) (2002), 4455-4472. - W. Gautschi, G. Mastroianni and Th. M. Rassias, Approximation and Computation: In Honor of Gradimir V. Milovanovic, Springer, New York, 2011.
- D. H. Hyers, G. Isac and Th. M. Rassias, Stability of Functional Equations in Several Variables, Birkhäuser Verlag, Boston, Basel, Berlin, 1998.
- D. H. Hyers, G. Isac and Th. M. Rassias, Topics in Nonlinear Analysis and Applications, World Scientific Publishing Co., Singapore, New Jersey, London, 1997.
- S.-M. Jung, Hyers-Ulam-Rassias Stability of Functional Equations in Mathematical Analysis, Hadronic Press Inc., Florida, 2001.
- G. V. Milovanovic, D. S. Mitrinovic and Th. M. Rassias, Topics in Polynomials: Extremal Problems, Inequalities, Zeros, World Scientific Publishing Co., Singapore, New Jersey, London, 1994.
- P. M. Pardalos, Th. M. Rassias and A. A. Khan, Nonlinear Analysis and Variational Problems, Springer Optimization and its Applications 35, Springer, Berlin, 2009.
- Th. M. Rassias, On the stability of the linear mapping in Banach spaces, Proceedings of the American Mathematical Society 72(1978), 297-300. [Translated in Chinese and published in: Mathematical Advance in Translation, Chinese Academy of Sciences 4 (2009), 382-384.]
- Th. M. Rassias, New characterizations of inner product spaces, Bulletin des Sciences Mathematiques, 108 (1984), 95-99.
- Th. M. Rassias, On the stability of functional equations and a problem of Ulam, Acta Applicandae Mathematicae 62(1) (2000), 23-130.
- Th. M. Rassias, Major trends in Mathematics, Newsletter European Math. Soc. 62 (2006), 13-14.[Translated in Chinese and published in:Mathematical Advance in Translation, Chinese Academy of Sciences 2 (2008), 172-174.
- Th. M. Rassias and J. Brzdek, Functional Equations in Mathematical Analysis, Springer, New York, 2011 (to appear).
- Th. M. Rassias and J. Simsa, Finite Sums Decompositions in Mathematical Analysis, John Wiley & Sons Ltd. (Wiley-Interscience Series in Pure and Applied Mathematics), Chichester, New York, Brisbane, Toronto, Singapore, 1995.