Tetrahedral-octahedral honeycomb
| Alternated cubic honeycomb | |
|---|---|
| Type | Uniform honeycomb |
| Family | Alternated hypercubic honeycomb |
| Schläfli symbol | h0{4,3,4} {3[4]} |
| Coxeter-Dynkin diagrams | or |
| Cell types | {3,3}, {3,4} |
| Face types | triangle {3} |
| Edge figure | [{3,3}.{3,4}]2 (rectangle) |
| Vertex figure | (cuboctahedron) |
| Cells/edge | [{3,3}.{3,4}]2 |
| Faces/edge | 4 {3} |
| Cells/vertex | {3,3}8+{3,4}6 |
| Faces/vertex | 24 {3} |
| Edges/vertex | 12 |
| Symmetry group | Fm3m |
| Coxeter groups | 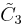 , [1+,4,3,4] (half) , [1+,4,3,4] (half)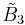 , [4,31,1] , [4,31,1]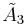 , [3[4]] , [3[4]] |
| Dual | rhombic dodecahedral honeycomb |
| Properties | vertex-transitive, edge-transitive, face-transitive |
The tetrahedral-octahedral honeycomb or alternated cubic honeycomb is a space-filling tessellation (or honeycomb) in Euclidean 3-space. It is composed of alternating octahedra and tetrahedra in a ratio of 1:2.
It is vertex-transitive with 8 tetrahedra and 6 octahedra around each vertex. It is edge-transitive with 2 tetrahedra and 2 octahedra alternating on each edge.
It is part of an infinite family of uniform tessellations called alternated hypercubic honeycombs, formed as an alternation of a hypercubic honeycomb and being composed of demihypercube and cross-polytope facets.
In this case of 3-space, the cubic honeycomb is alternated, reducing the cubic cells to tetrahedra, and the deleted vertices create octahedral voids. As such it can be represented by an extended Schläfli symbol h{4,3,4} as containing half the vertices of the {4,3,4} cubic honeycomb.
There's a similar honeycomb called gyrated tetrahedral-octahedral honeycomb which has layers rotated 60 degrees so half the edges have neighboring rather than alternating tetrahedra and octahedra.
This vertex arrangement is called the A3 lattice.[1]
Contents |
Images
Wireframe (perspective) |
This diagram shows an exploded view of the cells surrounding each vertex. |
Projection by folding
The alternated cubic honeycomb can be orthogonally projected into the planar square tiling by a geometric folding operation that maps two pairs of mirrors into each other. The projection of the alternated cubic honeycomb creates two offset copies of the square tiling vertex arrangement of the plane:
| Coxeter group |
Coxeter diagram |
Graph |
|---|---|---|
 |
alternated cubic honeycomb |
|
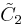 |
square tiling |
See also
Notes
References
- George Olshevsky, Uniform Panoploid Tetracombs, Manuscript (2006) (Complete list of 11 convex uniform tilings, 28 convex uniform honeycombs, and 143 convex uniform tetracombs)
- Branko Grünbaum, Uniform tilings of 3-space. Geombinatorics 4(1994), 49 - 56.
- Norman Johnson Uniform Polytopes, Manuscript (1991)
- Williams, Robert (1979). The Geometrical Foundation of Natural Structure: A Source Book of Design. Dover Publications, Inc. ISBN 0-486-23729-X.
- Critchlow, Keith (1970). Order in Space: A design source book. Viking Press. ISBN 0-500-34033-1.
- Kaleidoscopes: Selected Writings of H.S.M. Coxeter, edited by F. Arthur Sherk, Peter McMullen, Anthony C. Thompson, Asia Ivic Weiss, Wiley-Interscience Publication, 1995, ISBN 978-0-471-01003-6 [1]
- (Paper 22) H.S.M. Coxeter, Regular and Semi Regular Polytopes I, [Math. Zeit. 46 (1940) 380-407, MR 2,10] (1.9 Uniform space-fillings)
- (Paper 24) H.S.M. Coxeter, Regular and Semi-Regular Polytopes III, [Math. Zeit. 200 (1988) 3-45]
- A. Andreini, Sulle reti di poliedri regolari e semiregolari e sulle corrispondenti reti correlative (On the regular and semiregular nets of polyhedra and on the corresponding correlative nets), Mem. Società Italiana della Scienze, Ser.3, 14 (1905) 75–129.
- D. M. Y. Sommerville, An Introduction to the Geometry of n Dimensions. New York, E. P. Dutton, 1930. 196 pp. (Dover Publications edition, 1958) Chapter X: The Regular Polytopes
External links
- Architectural design made with Tetrahedrons and regular Pyramids based square.(2003)
- Richard Klitzing, 3D Euclidean Honeycombs, x3o3o *b4o - octet - O21
- Uniform Honeycombs in 3-Space: 11-Octet