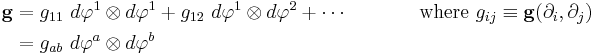Tetrad formalism
The tetrad formalism [1] is a non-coordinate approach to General Relativity.
In the tetrad formalism all tensors are represented in terms of a chosen basis, a set of four vectors called the tetrad. (When applied to theories with other than four dimensions, this approach is given other names; see also Cartan formalism). As a formalism rather than a separate theory, it does not make different predictions but does allow the relevant equations to be expressed differently.
The advantage of the tetrad formalism over the standard coordinate-based approach to GR lies in the ability to choose the tetrad basis to reflect important physical aspects of the spacetime.
Contents |
Mathematical details
In the tetrad formalism, a tetrad basis is chosen — a set of four independent vector fields 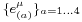 that together span the 4D vector tangent space at each point in spacetime. Here, spacetime means a four-dimensional, smooth, connected Lorentzian manifold
that together span the 4D vector tangent space at each point in spacetime. Here, spacetime means a four-dimensional, smooth, connected Lorentzian manifold  . All tensors of the theory are then expressed in this vector basis, by projecting them against members of the tetrad. For example, the spacetime metric itself can be transformed from a coordinate basis to the tetrad basis:
. All tensors of the theory are then expressed in this vector basis, by projecting them against members of the tetrad. For example, the spacetime metric itself can be transformed from a coordinate basis to the tetrad basis:
Popular tetrad bases include orthonormal tetrads and null tetrads. The latter are used frequently in problems dealing with radiation, and are the basis of the Newman-Penrose formalism.
From a mathematical point of view, the four vector fields 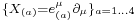 define a parallelization of
define a parallelization of 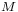 . Hence—in this case—the tangent bundle
. Hence—in this case—the tangent bundle 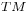 is diffeomorphic to the product manifolds
is diffeomorphic to the product manifolds 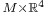 .
.
Relation to standard formalism
The standard formalism of differential geometry (and General Relativity) consists simply of using the coordinate tetrad in the tetrad formalism. The coordinate tetrad is the canonical set of vectors associated with the coordinate chart.
The coordinate tetrad is commonly denoted 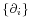 . These tangent vectors are usually defined as directional derivative operators; given a chart
. These tangent vectors are usually defined as directional derivative operators; given a chart 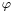 (which maps a subset of the manifold into coordinate space
(which maps a subset of the manifold into coordinate space 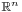 ) and any scalar field
) and any scalar field 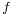 , the coordinate vectors are such that:
, the coordinate vectors are such that:
Any tensor can be written in terms of this tetrad (and its dual vector counterparts, which are defined such that ![\scriptstyle d\varphi^i[\partial_j]=\delta^i_j](/2012-wikipedia_en_all_nopic_01_2012/I/fe96a89ab7acb3fab3021dfad2f3927a.png) using the Kronecker delta). For example, the metric tensor can be expressed:
using the Kronecker delta). For example, the metric tensor can be expressed:
The involvement of the coordinate tetrad is not normally made explicit. Instead of writing tensor equations out fully (including tetrad elements and tensor products 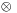 as above) only components of the tensors are mentioned. For example, the metric is written as "
as above) only components of the tensors are mentioned. For example, the metric is written as "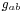 ". This is called abstract index notation.
". This is called abstract index notation.
Changing tetrad is a routine operation in the standard formalism, as it is involved in every coordinate transformation (i.e., changing from one coordinate tetrad basis to another). Switching between multiple coordinate charts is necessary because, except in trivial cases, it is not possible for a single coordinate chart to cover the entire manifold.
See also
- Frame bundle
- Orthonormal frame bundle
- Principal bundle
- Spin bundle
- Connection (mathematics)
- G-structure
- Spin manifold
- Spin structure
Notes
- ^ De Felice, F.; Clarke, C.J.S. (1990), p. 133
References
- De Felice, F.; Clarke, C.J.S. (1990), Relativity on Curved Manifolds (First published 1990 ed.), Cambridge University Press, ISBN 0-521-26639-4
- Benn, I.M.; Tucker, R.W. (1987), An introduction to Spinors and Geometry with Applications in Physics (First published 1987 ed.), Adam Hilger, ISBN 0-85274-169-3
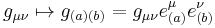
![\partial_i [f] \equiv \frac{\partial f \circ \varphi^{-1} }{\partial \varphi^i}](/2012-wikipedia_en_all_nopic_01_2012/I/afa2396cf838d866674d482e1e94f6dc.png)