Ternary numeral system

Numeral systems by culture
Hindu-Arabic numerals
Western Arabic (Hindu numerals)
Eastern Arabic
Indian family
Tamil		 Burmese
Khmer
Lao
Mongolian
Thai
East Asian numerals
Chinese
Japanese
Suzhou		 Korean
Vietnamese
Counting rods
Alphabetic numerals
Abjad
Armenian
Āryabhaṭa
Cyrillic		 Ge'ez
Greek
Georgian
Hebrew
Other systems
Aegean
Attic
Babylonian
Brahmi
Egyptian
Etruscan
Inuit		 Kharosthi
Mayan
Quipu
Roman
Sumerian
Urnfield
List of numeral system topics
Positional systems by base
Decimal (10)
2, 3, 4, 5, 6, 7, 8, 9, 11, 12, 13, 14, 15, 16, 20, 24, 30, 36, 60, 64
Non-positional system
Unary numeral system (Base 1)
List of numeral systems

Ternary (sometimes called trinary) is the base-3 numeral system. Analogous to a bit, a ternary digit is a trit (trinary digit). One trit contains 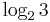\log_2 3 (about 1.58496) bits of information. Although ternary most often refers to a system in which the three digits 0, 1, and 2 are all whole numbers, the adjective also lends its name to the balanced ternary system, used in comparison logic and ternary computers.

Contents

Comparison to other radixes

Compared to decimal and binary

Representations of integer numbers in ternary do not get uncomfortably lengthy as quickly as in binary. For example, decimal 365 corresponds to binary 101101101 (9 digits) and to ternary 111112 (6 digits). However, they are still far less compact than the corresponding representations in bases such as decimal — see below for a compact way to codify ternary using nonary and septemvigesimal.

Numbers one to twenty-seven in standard ternary
Ternary 1 2 10 11 12 20 21 22 100
Binary 1 10 11 100 101 110 111 1000 1001
Decimal 1 2 3 4 5 6 7 8 9
Ternary 101 102 110 111 112 120 121 122 200
Binary 1010 1011 1100 1101 1110 1111 10000 10001 10010
Decimal 10 11 12 13 14 15 16 17 18
Ternary 201 202 210 211 212 220 221 222 1000
Binary 10011 10100 10101 10110 10111 11000 11001 11010 11011
Decimal 19 20 21 22 23 24 25 26 27
Powers of three in ternary
Ternary 1 10 100 1 000 10 000
Binary 1 11 1001 1 1011 101 0001
Decimal 1 3 9 27 81
Power 30 31 32 33 34
Ternary 100 000 1 000 000 10 000 000 100 000 000 1 000 000 000
Binary 1111 0011 10 1101 1001 1000 1000 1011 1 1001 1010 0001 100 1100 1110 0011
Decimal 243 729 2 187 6 561 19 683
Power 35 36 37 38 39

As for rational numbers, ternary offers a convenient way to represent one third (as opposed to its cumbersome representation as an infinite string of recurring digits in decimal); but a major drawback is that, in turn, ternary does not offer a finite representation for the most basic fraction: one half (and thus, neither for one quarter, one sixth, one eighth, one tenth, etc.), because 2 is not a prime factor of the base.

Fractions in ternary
Ternary 0.111111111111... 0.1 0.020202020202... 0.012101210121... 0.011111111111... 0.010212010212...
Binary 0.1 0.010101010101... 0.01 0.001100110011... 0.00101010101... 0.001001001001...
Decimal 0.5 0.333333333333... 0.25 0.2 0.166666666666... 0.142857142857...
Fraction 1/2 1/3 1/4 1/5 1/6 1/7
Ternary 0.010101010101... 0.01 0.002200220022... 0.002110021100... 0.002020202020... 0.002002002002...
Binary 0.001 0.000111000111... 0.000110011001... 0.000101110100... 0.000101010101... 0.000100111011...
Decimal 0.125 0.111111111111... 0.1 0.090909090909... 0.083333333333... 0.076923076923...
Fraction 1/8 1/9 1/10 1/11 1/12 1/13

Sum of the digits in ternary as opposed to binary

Whereas in binary the sum of all previous digit values before 2n can be found using the formula 2n-1, in ternary the following formula can be used: (3n-1)/2.

An example is where in binary the fourth digit has a value of 8, the sum of all the binary numbers before 8 can be found out using the above formula as 23-1, which is 7. In ternary the fourth digit has a value of 27 and the sum of all previous ternary numbers can be found out using the above formula, as (33-1)/2, which is 13.

The formula is 3n because we are counting to base 3 and we divide by 2 now because the maximum value of each digit is 2. The general formula for the nth digit it a base-N number is:

Nn

and the sum of previous digits:

(Nn-1)/(N-1)

Compact ternary representation: base 9 and 27

Nonary (base 9, each digit is two ternary digits) or septemvigesimal (base 27, each digit is three ternary digits) is often used, similar to how octal and hexadecimal systems are used in place of binary.

Practical usage

A base-three system is used in Islam to keep track of counting Tasbih to 99 or to 100 on a single hand for counting prayers (as alternative for the Misbaha). The benefit—apart from allowing a single hand to count up to 99 or to 100—is that counting doesn't distract the mind too much since the counter needs only to divide Tasbihs into groups of three.

A rare "ternary point" is used to denote fractional parts of an inning in baseball. Since each inning consists of three outs, each out is considered one third of an inning and is denoted as .1. For example, if a player pitched all of the 4th, 5th and 6th innings, plus 2 outs of the 7th inning, his Innings pitched column for that game would be listed as 3.2, meaning 3⅔. In this usage, only the fractional part of the number is written in ternary form.

Ternary numbers can be used to convey self-similar structures like the Sierpinski triangle or the Cantor set conveniently. Additionally, it turns out that the ternary representation is useful for defining the Cantor set and related point sets, because of the way the Cantor set is constructed. The Cantor set consists of the points from 0 to 1 that have a ternary expression that does not contain any instance of the digit 1. [1][2] Any terminating expansion in the ternary system is equivalent to the expression that is identical up to the term preceeding the last non-zero term followed by the term one less than the last nonzero term of the first expression, followed by an infinite tail of twos. For example: .1020 is equivalent to .1012222... because the expansions are the same until the "two" of the first expression, the two was decremented in the second expansion, and trailing zeros were replaced with trailing twos in the second expression.

Ternary is the integer base with the highest radix economy, followed closely by binary and quaternary. It has been used for some computing systems because of this efficiency. It is also used to represent 3 option trees, such as phone menu systems, which allow a simple path to any branch.

Tryte

Some ternary computers such as the Setun defined a tryte to be 6 trits, analogous to the binary byte.[3]

See also

Notes

  1. ^ Mohsen Soltanifar, On A sequence of cantor Fractals, Rose Hulman Undergraduate Mathematics Journal, Vol 7, No 1, paper 9, 2006.
  2. ^ Mohsen Soltanifar, A Different Description of A Family of Middle-a Cantor Sets, American Journal of Undergraduate Research, Vol 5, No 2, pp 9–12, 2006.
  3. ^ Brousentsov, N. P.; Maslov, S. P.; Ramil Alvarez, J.; Zhogolev, E.A.. "Development of ternary computers at Moscow State University". http://www.computer-museum.ru/english/setun.htm. Retrieved 20 January 2010. 

References

External links

Uninterpreted
Numeric
Text
Pointer
Composite
Other
Related topics