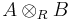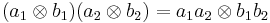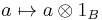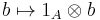Tensor product of algebras
In mathematics, the tensor product of two R-algebras is also an R-algebra. This gives us a tensor product of algebras. The special case R = Z gives us a tensor product of rings, since rings may be regarded as Z-algebras.
Let R be a commutative ring and let A and B be R-algebras. Since A and B may both be regarded as R-modules, we may form their tensor product
which is also an R-module. We can give the tensor product the structure of an algebra by defining[1]
and then extending by linearity to all of A⊗RB. This product is easily seen to be R-bilinear, associative, and unital with an identity element given by 1A⊗1B,[2] where 1A and 1B are the identities of A and B. If A and B are both commutative then the tensor product is as well.
The tensor product turns the category of all R-algebras into a symmetric monoidal category.
There are natural homomorphisms of A and B to A⊗RB given by[3]
These maps make the tensor product a coproduct in the category of commutative R-algebras. (The tensor product is not the coproduct in the category of all R-algebras. There the coproduct is given by a more general free product of algebras).
The tensor product of algebras is of constant use in algebraic geometry: working in the opposite category to that of commutative R-algebras, it provides pullbacks of affine schemes, otherwise known as fiber products.
See also
Notes
References
- Kassel, Christian (1995), Quantum groups, Graduate texts in mathematics, 155, Springer, ISBN 9780387943701.