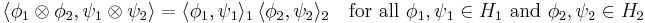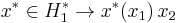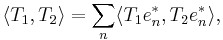Tensor product of Hilbert spaces

In mathematics, and in particular functional analysis, the tensor product of Hilbert spaces is a way to extend the tensor product construction so that the result of taking a tensor product of two Hilbert space is another Hilbert space. Roughly speaking, the tensor product is the completion of the ordinary tensor product. This is a special case of a topological tensor product.

1 Definition
2 Properties
3 Examples and applications
4 References

Definition

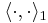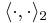Since Hilbert spaces have inner products, one would like to introduce an inner product, and therefore a topology, on the tensor product that arise naturally from those of the factors. Let H₁ and H₂ be two Hilbert spaces with inner products $\langle \cdot,\cdot\rangle_1$ and $\langle \cdot,\cdot\rangle_2$ , respectively. Construct the tensor product of H₁ and H₂ as vector spaces as explained in the article on tensor products. We can turn this vector space tensor product into an inner product space by defining

$\langle\phi_1\otimes\phi_2,\psi_1\otimes\psi_2\rangle = \langle\phi_1,\psi_1\rangle_1 \, \langle\phi_2,\psi_2\rangle_2 \quad \mbox{for all } \phi_1,\psi_1 \in H_1 \mbox{ and } \phi_2,\psi_2 \in H_2$

and extending by linearity. That this inner product is the natural one is justified by the identification of scalar-valued bilinear maps on H₁ × H₂ and linear functionals on their vector space tensor product. Finally, take the completion under this inner product. The resulting Hilbert space is the tensor product of H₁ and H₂.

Explicit construction

The tensor product can also be defined without appealing to the metric space completion. If H₁ and H₂ are two Hilbert spaces, one associates to every simple tensor product $x_1 \otimes x_2$ the rank one operator

$x^* \in H_1^* \rightarrow x^*(x_1) \, x_2$

from H₁^∗ to H₂, and this extends to a linear identification between $H_1 \otimes H_2$ and the space of finite rank operators from H₁^∗ to H₂. The finite rank operators are embedded in the Hilbert space HS(H₁^∗, H₂) of Hilbert-Schmidt operators from H₁^∗ to H₂. The scalar product in HS(H₁^∗, H₂) is given by

$\langle T_1, T_2 \rangle = \sum_n \langle T_1 e_n^*, T_2 e_n^* \rangle,$

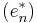where $(e_n^*)$ is an arbitrary orthonormal basis of H₁^∗.

Under the preceding identification, one can define the Hilbertian tensor product of H₁ and H₂, that is isometrically and linearly isomorphic to HS(H₁^∗, H₂).

Universal property

The Hilbert tensor product 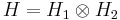$H=H_1\otimes H_2$ is characterized by the following universal property (Kadison & Ringrose 1983, Theorem 2.6.4):

There is a weakly Hilbert-Schmidt mapping p : H₁ × H₂ → H such that, given any weakly Hilbert-Schmidt mapping L : H₁ × H₂ → K to a Hilbert space K, there is a unique bounded operator T from H to K such that L = Tp.

As with any universal property, this characterizes the tensor product H up to isomorphism. The same universal property, with obvious modifications, also applies for the tensor product of any finite number of Hilbert spaces.

Infinite tensor products

If 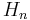$H_n$ is a collection of Hilbert spaces and 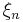$\xi_n$ is a collection of unit vectors in these Hilbert spaces then the incomplete tensor product (or Guichardet tensor product) is the 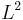$L^2$ completion of the set of all finite linear combinations of simple tensor vectors 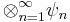$\otimes_{n=1}^{\infty} \psi_n$ where all but finitely many of the 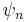$\psi_n$ 's equal the corresponding 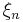$\xi_n$ ^[1].

Operator algebras

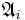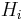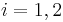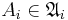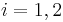Let $\mathfrak{A}_i$ be the von Neumann algebra of bounded operators on $H_i$ for $i=1,2$ . Then the von Neumann tensor product of the von Neumann algebras is the strong completion of the set of all finite linear combinations of simple tensor products $A_1\otimes A_2$ where $A_i \in \mathfrak{A}_i$ for $i=1,2$ . This is exactly equal to the von Neumann algebra of bounded operators of $H_1\otimes H_2$ . 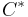Unlike for Hilbert spaces, one may take infinite tensor products of von Neumann algebras, and for that matter $C^*$ -algebras of operators, without defining reference states^[1]. This is one advantage of the "algebraic" method in quantum statistical mechanics.

Properties

If H₁ and H₂ have orthonormal bases {φ_k} and {ψ_l}, respectively, then {φ_k ⊗ ψ_l} is an orthonormal basis for H₁ ⊗ H₂. In particular, the Hilbert dimension of the tensor product is the product (as cardinal numbers) of the Hilbert dimensions.

Examples and applications

The following examples show how tensor products arise naturally.

Given two measure spaces X and Y, with measures μ and ν respectively, one may look at L²(X × Y), the space of functions on X × Y that are square integrable with respect to the product measure μ × ν. If f is a square integrable function on X, and g is a square integrable function on Y, then we can define a function h on X × Y by h(x,y) = f(x) g(y). The definition of the product measure ensures that all functions of this form are square integrable, so this defines a bilinear mapping L²(X) × L²(Y) → L²(X × Y). Linear combinations of functions of the form f(x) g(y) are also in L²(X × Y). It turns out that the set of linear combinations is in fact dense in L²(X × Y), if L²(X) and L²(Y) are separable. This shows that L²(X) ⊗ L²(Y) is isomorphic to L²(X × Y), and it also explains why we need to take the completion in the construction of the Hilbert space tensor product.

Similarly, we can show that L²(X; H), denoting the space of square integrable functions X → H, is isomorphic to L²(X) ⊗ H if this space is separable. The isomorphism maps f(x) ⊗ φ ∈ L²(X) ⊗ H to f(x)φ ∈ L²(X; H). We can combine this with the previous example and conclude that L²(X) ⊗ L²(Y) and L²(X × Y) are both isomorphic to L²(X; L²(Y)).

Tensor products of Hilbert spaces arise often in quantum mechanics. If some particle is described by the Hilbert space H₁, and another particle is described by H₂, then the system consisting of both particles is described by the tensor product of H₁ and H₂. For example, the state space of a quantum harmonic oscillator is L²(R), so the state space of two oscillators is L²(R) ⊗ L²(R), which is isomorphic to L²(R²). Therefore, the two-particle system is described by wave functions of the form φ(x₁, x₂). A more intricate example is provided by the Fock spaces, which describe a variable number of particles.

References

Kadison, Richard V.; Ringrose, John R. (1997), Fundamentals of the theory of operator algebras. Vol. I, Graduate Studies in Mathematics, 15, Providence, R.I.: American Mathematical Society, ISBN 978-0-8218-0819-1, MR 1468229 .
Weidmann, Joachim (1980), Linear operators in Hilbert spaces, Graduate Texts in Mathematics, 68, Berlin, New York: Springer-Verlag, ISBN 978-0-387-90427-6, MR 566954 .

^ ^a ^b Bratteli, O. and Robinson, D: Operator Algebras and Quantum Statistical Mechanics v.1, 2nd ed., page 144. Springer-Verlag, 2002.