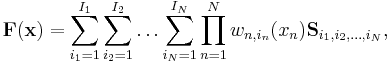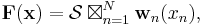Tensor product model transformation
The tensor product (TP) model transformation originally proposed for control design by Baranyi [1] [2] is capable of numerically reconstructing the higher-order singular value decomposition (HOSVD) of continuous multi-variable functions. The HOSVD of functions is defined by Baranyi et al. in [3]. Further, it is capable of reconstructing various special kinds of convex TP structure of the given functions (especially developed for linear matrix inequality based control design).
Contents |
Properties of the TP model transformation
- It is a non-heuristic and tractable numerical method firstly proposed in control theory [1][2]. Its free MATLAB implementation is downloadable at [1]
- It transforms the given function into finite element TP structure. If this structure does not exist, then the transformation gives an approximation under the constrain on the number of elements.
- The given function can be a matrix or tensor, and it is irrelevant whether it is given by closed analytical formulas or by neural network, fuzzy logic rule base etc.
- It reconstruct the HOSVD of the given function. The HOSVD of functions are defined in [3]. This concept is based on the analogy of tensor HOSVD. The key difference is that instead of singular matrices we define singular functions. The higher-order singular values have the same meaning. All the advantages of tensor HOSVD can be carried over to function HOSVD. In the same way the main component analysis of functions can also be investigated in this concept. It is proven by Szeidl [4] that the TP model transformation numerical reconstructs or implements the HOSVD of functions.
- The TP model transformation is capable of performing trade-off between complexity and accuracy of TP functions via discarding the higher-order singular values, in the same manner as the tensor HOSVD is used for complexity reduction.
- The TP model transformation is originally developed for qLPV dynamic models. It hence, defines the HOSVD based canonical form of qLPV models. It is also applicable to investigate the main components of the given qLPV model.
- The TP model transformation is capable of generating various convex TP function. It has a special role in dynamic control design theory. For further details about control, please visit: the role of the TP model transformation in system control design.
Definitions
- The TP structure in general
- Assume a given multi-variable continuous function
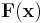 , where vector
, where vector 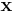 is an element of the closed hypercube
is an element of the closed hypercube ![\Omega=[a_1,b_1]\times[a_2,b_2]\times\cdot\times[a_N,b_N]\subset R^N](/2012-wikipedia_en_all_nopic_01_2012/I/6bfbf4b8fe29bf2c22f7f8e96dd82dae.png) . Note that
. Note that 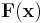 can be matrix or even tensor. In the followings we assume
can be matrix or even tensor. In the followings we assume 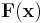 is a matrix with the size of
is a matrix with the size of 
- Finite element TP functions
- We say TP model for brevity.
 is given for any parameter
is given for any parameter 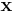 as the parameter varying combination of bounded number of constant matrices
as the parameter varying combination of bounded number of constant matrices 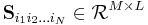 as
as
that is with compact tensor notation:
where the (N+2)-dimensional coefficient tensor 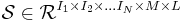 is constructed from matrices
is constructed from matrices 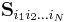 and row vector
and row vector ![\mathbf{w}_n(x_n)\in [0,1], (i_n=1 \ldots I_n)](/2012-wikipedia_en_all_nopic_01_2012/I/2a74935a923cb696335ab326fa30f550.png) contains one variable and continuous weighting functions
contains one variable and continuous weighting functions ![w_{n,i_n}(x_n)\in [0,1],(i_n=1 \ldots I_n)](/2012-wikipedia_en_all_nopic_01_2012/I/64039bd1c66a1a237b60f03ff3417caf.png) . The function
. The function 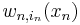 is the
is the 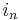 -th weighting function defined on the
-th weighting function defined on the  -th dimension of
-th dimension of  , and
, and 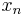 is the
is the  -th element of vector
-th element of vector 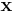 . The dimensions of
. The dimensions of  are respectively assigned to the elements of the parameter vector
are respectively assigned to the elements of the parameter vector 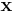 . For tensor operations see the works of Lathauwer [5] on HOSVD.
. For tensor operations see the works of Lathauwer [5] on HOSVD.
- Convex TP functions
- The TP function is convex if its weighting functions satisfy
![\forall n,i,x_n�: w_{n,i}(x_n)\in[0,1],](/2012-wikipedia_en_all_nopic_01_2012/I/8e0956890fe970b67c222197586f51a3.png)
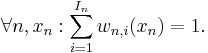
This actually means that the function  is within the convex hull, defined by constant matrices
is within the convex hull, defined by constant matrices 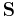 stored in tensor
stored in tensor 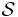 , for all
, for all 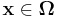 . The TP model transformation is capable of generating various convex TP representation of a given function. Further details could be found in [6] [7] [8] and in external links below.
. The TP model transformation is capable of generating various convex TP representation of a given function. Further details could be found in [6] [7] [8] and in external links below.
References
- ^ a b P. Baranyi and D. Tikk and Y. Yam and R. J. Patton (2003). "From Differential Equations to PDC Controller Design via Numerical Transformation". Computers in Industry, Elsevier Science 51: 281–297.
- ^ a b P. Baranyi (April 2004). "TP model transformation as a way to LMI based controller design". IEEE Transaction on Industrial Electronics 51 (2): 387–400.
- ^ a b P. Baranyi and L. Szeidl and P. Várlaki and Y. Yam (July 3–5 2006). Definition of the HOSVD-based canonical form of polytopic dynamic models. pp. 660–665.
- ^ L. Szeidl and P. Várlaki (2009). "HOSVD Based Canonical Form for Polytopic Models of Dynamic Systems". Journal of Advanced Computational Intelligence and Intelligent Informatics 13 (1): 52–60.
- ^ Lieven De Lathauwer and Bart De Moor and Joos Vandewalle (2000). "A Multilinear Singular Value Decomposition". Journal on Matrix Analysis and Applications 21 (4): 1253–1278.
- ^ P. Baranyi (May-June 2005). "Tensor-Product Model-Based Control of Two-Dimensional Aeroelastic System". Journal of Guidance, Control, and Dynamics 29 (2): 391–400.
- ^ P. Baranyi (May-June 2005). "Output Feedback Control of Two-Dimensional Aeroelastic System". Journal of Guidance, Control, and Dynamics 29 (3): 762–767.
- ^ P.Baranyi, Z. Petres, P.L. Várkonyi, P.Korondi and Y.Yam (2006). "Determination of Different Polytopic Models of the Prototypical Aeroelastic Wing Section by TP Model Transformation". Journal of Advanced Computational Intelligence and Intelligent Informatics 10 (4): 486–893. ISSN 1343-0130.