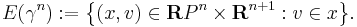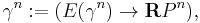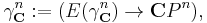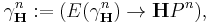Tautological line bundle
The canonical or tautological line bundle on a projective space appears frequently in mathematics, often in the study of characteristic classes. Note that there is possible confusion with the theory of the canonical class in algebraic geometry; for which reason the name tautological is preferred in some contexts.
For generalizations to Grassmannians, see also tautological bundle.
Contents |
Definition
Form the cartesian product 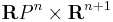 , with the first factor denoting real projective n-space. We consider the subset
, with the first factor denoting real projective n-space. We consider the subset
We have an obvious projection map 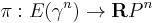 , with
, with 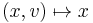 . Each fibre of
. Each fibre of  is then the line
is then the line  inside Euclidean (n+1)-space. Giving each fibre the induced vector space structure we obtain the bundle
inside Euclidean (n+1)-space. Giving each fibre the induced vector space structure we obtain the bundle
the canonical line bundle over 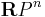 .
.
Complex and quaternionic cases
The above definition continues to makes sense if we replace the field 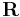 by either the complex numbers
by either the complex numbers 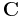 or the quaternions Thus we obtain the complex line bundle
or the quaternions Thus we obtain the complex line bundle
whose fibres are isomorphic to 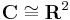 , and the quaternionic line bundle
, and the quaternionic line bundle
whose fibres are isomorphic to 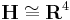 .
.
Tautological line bundle in algebraic geometry
In algebraic geometry, this notion exists over any commutative unital ring.
Over a field, its dual line bundle is the line bundle associated to the hyperplane divisor H, whose global sections are the linear forms. Its Chern class is -H. This is an example of an anti-ample line bundle.
Facts
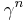 is locally trivial but not trivial, for
is locally trivial but not trivial, for 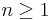 .
.
In fact, it is straightforward to show that, for 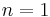 , the real canonical line bundle is none other than the well-known bundle whose total space is the Möbius strip. For a full proof of the above fact, see.[1]
, the real canonical line bundle is none other than the well-known bundle whose total space is the Möbius strip. For a full proof of the above fact, see.[1]
See also
References
- ^ J. Milnor & J. Stasheff, Characteristic Classes, Princeton, 1974.
- [M+S] J. Milnor & J. Stasheff, Characteristic Classes, Princeton, 1974.