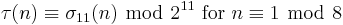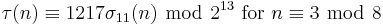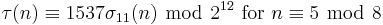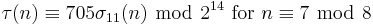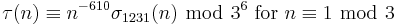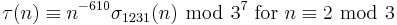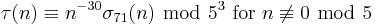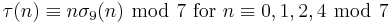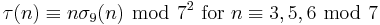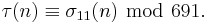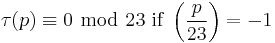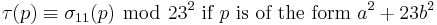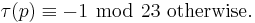Tau-function
The Ramanujan tau function, studied by Ramanujan (1916), is the function 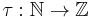 defined by the following identity:
defined by the following identity:
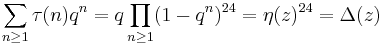 ,
,
where 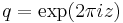 with
with 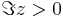 and
and 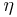 is the Dedekind eta function and the function
is the Dedekind eta function and the function 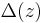 is a holomorphic cusp form of weight 12 and level 1, known as the discriminant modular form.
is a holomorphic cusp form of weight 12 and level 1, known as the discriminant modular form.
Contents |
Values
The first few values of the tau function are given in the following table (sequence A000594 in OEIS):
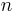 |
1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
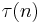 |
1 | −24 | 252 | −1472 | 4830 | −6048 | −16744 | 84480 | −113643 | −115920 | 534612 | −370944 | −577738 | 401856 | 1217160 | 987136 |
Ramanujan's conjectures
Ramanujan (1916) observed, but could not prove, the following three properties of 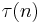 :
:
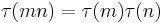 if
if 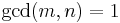 (meaning that
(meaning that 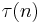 is a multiplicative function)
is a multiplicative function)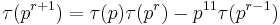 for p prime and r>0.
for p prime and r>0.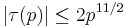 for all primes p.
for all primes p.
The first two properties were proved by Mordell (1917) and the third one, called the Ramanujan conjecture, was proved by Deligne in 1974 as a consequence of his proof of the Weil conjectures.
Congruences for the tau function
For k ∈ Z and n ∈ Z>0, define σk(n) as the sum of the k-th powers of the divisors of n. The tau functions satisfies several congruence relations; many of them can be expressed in terms of σk(n). Here are some:[1]
For p ≠ 23 prime, we have[1][7]
Conjectures on 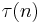
- Suppose that
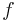 is a weight
is a weight 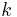 integer newform and the Fourier coefficients
integer newform and the Fourier coefficients 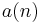 are integers. Consider the problem: If
are integers. Consider the problem: If 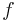 does not have complex multiplication, prove that almost all primes
does not have complex multiplication, prove that almost all primes 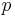 have the property that
have the property that 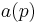 ≠
≠ 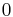 mod
mod 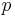 . Indeed, most primes should have this property, and hence they are called ordinary. Despite the big advances by Deligne and Serre on Galois representations, which determine
. Indeed, most primes should have this property, and hence they are called ordinary. Despite the big advances by Deligne and Serre on Galois representations, which determine 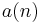 mod
mod 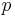 for
for 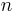 coprime to
coprime to 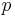 , we do not have any clue as to how to compute
, we do not have any clue as to how to compute 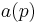 mod
mod 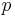 .The only theorem in this regard is Elkies' famous result for modular elliptic curves, which indeed guarantees that there are infinitely many primes
.The only theorem in this regard is Elkies' famous result for modular elliptic curves, which indeed guarantees that there are infinitely many primes 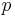 for which
for which 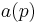 =
= 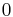 , which in turn is obviously
, which in turn is obviously 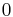 mod
mod 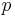 . We do not know any examples of non-CM
. We do not know any examples of non-CM 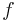 with weight
with weight 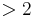 for which
for which 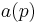 ≠
≠ 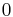 mod
mod 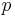 for infinitely many primes
for infinitely many primes 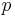 (although it should be true for almost all
(although it should be true for almost all 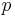 ). We also do not know any examples where
). We also do not know any examples where 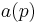 =
= 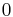 mod
mod 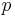 for infinitely many
for infinitely many 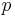 . Some people had begun to doubt whether
. Some people had begun to doubt whether 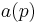 =
= 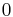 mod
mod 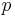 indeed for infinitely many
indeed for infinitely many 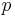 . As evidence, many provided Ramanujan's
. As evidence, many provided Ramanujan's 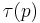 (case of weight
(case of weight 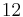 ). The largest known
). The largest known 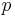 for which
for which 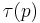 =
= 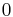 mod
mod 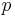 is
is 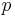 =
= 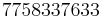 . The only solutions to the equation
. The only solutions to the equation 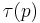

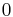 mod
mod 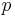 are
are 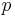 =
= 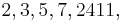 and
and 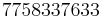 up to
up to 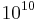 [9]
[9] - Lehmer (1947) conjectured that
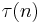 ≠
≠ 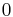 for all
for all 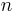 , an assertion sometimes known as Lehmer's conjecture. Lehmer verified the conjecture for
, an assertion sometimes known as Lehmer's conjecture. Lehmer verified the conjecture for 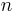 <
< 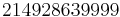 (Apostol 1997, p. 22). The following table summarizes progress on finding successively larger values of
(Apostol 1997, p. 22). The following table summarizes progress on finding successively larger values of 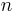 for which this condition holds.
for which this condition holds.
| n | reference |
|---|---|
| 3316799 | Lehmer (1947) |
| 214928639999 | Lehmer (1949) |
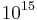 |
Serre (1973, p. 98), Serre (1985) |
| 1213229187071998 | Jennings (1993) |
| 22689242781695999 | Jordan and Kelly (1999) |
| 22798241520242687999 | Bosman (2007) |
Notes
- ^ a b Page 4 of Swinnerton-Dyer 1973
- ^ a b c d Due to Kolberg 1962
- ^ a b Due to Ashworth 1968
- ^ Due to Lahivi
- ^ a b Due to D. H. Lehmer
- ^ Due to Ramanujan 1916
- ^ Due to Wilton 1930
- ^ Due to J.-P. Serre 1968, Section 4.5
- ^ Due to N. Lygeros and O. Rozier 2010
References
- Apostol, T. M. (1997), "Modular Functions and Dirichlet Series in Number Theory", New York: Springer-Verlag 2nd ed.
- Ashworth, M. H. (1968), Congruence and identical properties of modular forms (D. Phil. Thesis, Oxford)
- Kolberg, O. (1962), "Congruences for Ramanujan's function τ(n)", Arbok Univ. Bergen Mat.-Natur. Ser. (11), MR0158873
- Lygeros, N. (2010), "A New Solution to the Equation τ(p) ≡ 0 (mod p)", Journal of Integer Sequences 13: Article 10.7.4, http://www.cs.uwaterloo.ca/journals/JIS/VOL13/Lygeros/lygeros5.pdf
- Mordell, Louis J. (1917), "On Mr. Ramanujan's empirical expansions of modular functions.", Proceedings of the Cambridge Philosophical Society 19: 117–124, JFM 46.0605.01, http://www.archive.org/stream/proceedingsofcam1920191721camb#page/n133
- Newman, M. (1972), "A table of τ (p) modulo p, p prime, 3 ≤ p ≤ 16067", National Bureau of Standards.
- Rankin, Robert A. (1988), "Ramanujan's tau-function and its generalizations", in Andrews, George E., Ramanujan revisited (Urbana-Champaign, Ill., 1987), Boston, MA: Academic Press, pp. 245–268, ISBN 978-0-12-058560-1, MR938968, http://books.google.com/books?id=GJUEAQAAIAAJ
- Ramanujan, Srinivasa (1916), "On certain arithmetical functions", Trans. Cambridge Philos. Soc. 22 (9): 159–184, MR2280861
- Serre, J-P. (1968), "Une interprétation relative à la fonction
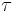 de Ramanujan", Séminaire Delange-Pisot-Poitou 14
de Ramanujan", Séminaire Delange-Pisot-Poitou 14 - Swinnerton-Dyer, H. P. F. (1973), "On ℓ-adic representations and congruences for coefficients of modular forms", in Kuyk, Willem; Serre, Jean-Pierre, Modular functions of one variable, III, Lecture Notes in Mathematics, 350, pp. 1–55, ISBN 978-3-540-06483-1, MR0406931, http://www.springerlink.com/content/978-3-540-06483-1
- Wilton, J. R. (1930), "Congruence properties of Ramanujan's function τ(n)", Proc. Lond. Math. Soc. 31: 1–10, doi:10.1112/plms/s2-31.1.1