Orbital period
The orbital period is the time taken for a given object to make one complete orbit about another object.
When mentioned without further qualification in astronomy this refers to the sidereal period of an astronomical object, which is calculated with respect to the stars.
There are several kinds of orbital periods for objects around the Sun (or other celestial objects):
- The sidereal period is the temporal cycle that it takes an object to make one full orbit, relative to the stars. This is considered to be an object's true orbital period.
- The synodic period is the temporal interval that it takes for an object to reappear at the same point in relation to two other objects (linear nodes), e.g., when the Moon relative to the Sun as observed from Earth returns to the same illumination phase. The synodic period is the time that elapses between two successive conjunctions with the Sun–Earth line in the same linear order. The synodic period differs from the sidereal period due to the Earth's orbiting around the Sun.
- The draconitic period, or draconic period, is the time that elapses between two passages of the object through its ascending node, the point of its orbit where it crosses the ecliptic from the southern to the northern hemisphere. This period differes from the sidereal period because both the orbital plane of the object and the plane of the ecliptic precess with respect to the fixed stars, so their intersection, the line of nodes, also precesses with respect to the fixed stars. Although the plane of the ecliptic is often held fixed at the position it occupied at a specific epoch, the orbital plane of the object still precesses causing the draconitic period to differ from the sidereal period.
- The anomalistic period is the time that elapses between two passages of an object at its periapsis (in the case of the planets in the solar system, called the perihelion), the point of its closest approach to the attracting body. It differs from the sidereal period because the object's semimajor axis typically advances slowly.
- Also, the Earth's tropical period (or simply its "year") is the time that elapses between two alignments of its axis of rotation with the Sun, also viewed as two passages of the object at right ascension zero. One Earth year has a slightly shorter interval than the solar orbit (sidereal period) because the inclined axis and equatorial plane slowly precesses (rotates in sidereal terms), realigning before orbit completes with an interval equal to the inverse of the precession cycle (about 25,770 years).
Contents |
Relation between the sidereal and synodic periods
Table of synodic periods in the Solar System, relative to Earth:
| Sidereal Period (a) | Synodic Period (a) | Synodic Period (d) | |
| Solar surface | 0.069[1] (25.3 days) | 0.074 | 27.3 |
| Mercury | 0.241 (88.0 days) | 0.317 | 115.9 |
| Venus | 0.615 (225 days) | 1.599 | 583.9 |
| Earth | 1 | — | — |
| Moon | 0.0748 | 0.0809 | 29.5306 |
| Mars | 1.881 | 2.135 | 779.9 |
| 4 Vesta | 3.629 | 1.380 | 504.0 |
| 1 Ceres | 4.600 | 1.278 | 466.7 |
| 10 Hygiea | 5.557 | 1.219 | 445.4 |
| Jupiter | 11.86 | 1.092 | 398.9 |
| Saturn | 29.46 | 1.035 | 378.1 |
| Uranus | 84.32 | 1.012 | 369.7 |
| Neptune | 164.8 | 1.006 | 367.5 |
| 134340 Pluto | 248.1 | 1.004 | 366.7 |
| 136199 Eris | 557 | 1.002 | 365.9 |
| 90377 Sedna | 12050 | 1.00001 | 365.1 |
In the case of a planet's moon, the synodic period usually means the Sun-synodic period. That is to say, the time it takes the moon to complete its illumination phases, completing the solar phases for an observer on the planet's surface —the Earth's motion does not determine this value for other planets, because an Earth observer is not orbited by the moons in question. For example, Deimos' synodic period is 1.2648 days, 0.18% longer than Deimos' sidereal period of 1.2624 d.
Calculation
Small body orbiting a central body
In astrodynamics the orbital period 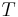 of a small body orbiting a central body in a circular or elliptic orbit is:
of a small body orbiting a central body in a circular or elliptic orbit is:
where:
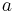 is length of orbit's semi-major axis,
is length of orbit's semi-major axis,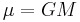 is the standard gravitational parameter,
is the standard gravitational parameter, is the gravitational constant,
is the gravitational constant,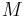 the mass of the central body.
the mass of the central body.
Note that for all ellipses with a given semi-major axis the orbital period is the same, regardless of eccentricity.
Orbital period as a function of central body's density
For the Earth (and any other spherically symmetric body with the same average density) as central body we get:
and for a body of water
T in hours, with R the radius of the body.
Thus, as an alternative for using a very small number like G, the strength of universal gravity can be described using some reference material, like water: the orbital period for an orbit just above the surface of a spherical body of water is 3 hours and 18 minutes. Conversely, this can be used as a kind of "universal" unit of time.
For the Sun as central body we simply get
T in years, with a in astronomical units. This is the same as Kepler's Third Law
Two bodies orbiting each other
In celestial mechanics when both orbiting bodies' masses have to be taken into account the orbital period 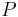 can be calculated as follows:
can be calculated as follows:
where:
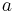 is the sum of the semi-major axes of the ellipses in which the centers of the bodies move, or equivalently, the semi-major axis of the ellipse in which one body moves, in the frame of reference with the other body at the origin (which is equal to their constant separation for circular orbits),
is the sum of the semi-major axes of the ellipses in which the centers of the bodies move, or equivalently, the semi-major axis of the ellipse in which one body moves, in the frame of reference with the other body at the origin (which is equal to their constant separation for circular orbits),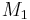 and
and 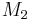 are the masses of the bodies,
are the masses of the bodies, is the gravitational constant.
is the gravitational constant.
Note that the orbital period is independent of size: for a scale model it would be the same, when densities are the same (see also Orbit#Scaling in gravity).
In a parabolic or hyperbolic trajectory the motion is not periodic, and the duration of the full trajectory is infinite.
Earth orbits
| orbit | center-to-center distance |
altitude above the Earth's surface |
speed | period/time in space | specific orbital energy |
|---|---|---|---|---|---|
| minimum sub-orbital spaceflight (vertical) | 6,500 km | 100 km | 0.0 km/s | just reaching space | -61.3 MJ/kg |
| ICBM | up to 7,600 km | up to 1,200 km | 6 to 7 km/s | time in space: 25 min | -27.9 MJ/kg |
| Low Earth orbit | 6,600 to 8,400 km | 200 to 2,000 km | circular orbit: 6.9 to 7.8 km/s elliptic orbit: 6.5 to 8.2 km/s |
89 to 128 min | -17.0 MJ/kg |
| Molniya orbit | 6,900 to 46,300 km | 500 to 39,900 km | 1.5 to 10.0 km/s | 11 h 58 min | -4.7 MJ/kg |
| GEO | 42,000 km | 35,786 km | 3.1 km/s | 23 h 56 min | -4.6 MJ/kg |
| Orbit of the Moon | 363,000 to 406,000 km | 357,000 to 399,000 km | 0.97 to 1.08 km/s | 27.3 days | -0.5 MJ/kg |
Binary stars
| Binary star | Orbital period |
|---|---|
| AM Canum Venaticorum | 17.146 minutes |
| Beta Lyrae AB | 12.9075 days |
| Alpha Centauri AB | 79.91 years |
| Proxima Centauri - Alpha Centauri AB | 500,000 years or more |
Notes
- ^ The motion of the solar surface is not purely gravitational and therefore does not follow Kepler's laws of motion
See also
- Geosynchronous orbit derivation
- Sidereal time
- Sidereal year
- Opposition (astronomy)
- List of periodic comets
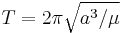
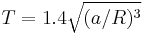
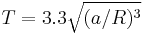
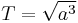
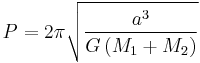
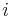
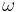
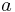
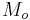
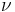
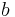
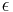
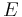
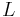
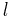
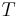 Orbital period
Orbital period