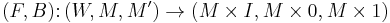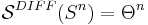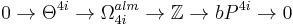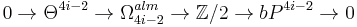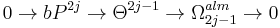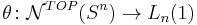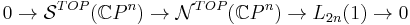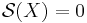Surgery exact sequence
In the mathematical surgery theory the surgery exact sequence is the main technical tool to calculate the surgery structure set of a compact manifold in dimension 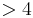 . The surgery structure set
. The surgery structure set 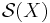 of a compact
of a compact  -dimensional manifold
-dimensional manifold  is a pointed set which classifies
is a pointed set which classifies  -dimensional manifolds within the homotopy type of
-dimensional manifolds within the homotopy type of  .
.
The basic idea is that in order to calculate 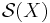 it is enough to understand the other terms in the sequence, which are usually easier to determine. These are on one hand the normal invariants which form generalized cohomology groups, and hence one can use standard tools of algebraic topology to calculate them at least in principle. On the other hand there are the L-groups which are defined algebraically in terms of quadratic forms or in terms of chain complexes with quadratic structure. A great deal is known about these groups. Another part of the sequence are the surgery obstruction maps from normal invariants to the L-groups. For these maps there are certain characteristic classes formulas, which enable to calculate them in some cases. Knowledge of these three components, that means: the normal maps, the L-groups and the surgery obstruction maps is enough to determine the structure set (at least up to extension problems).
it is enough to understand the other terms in the sequence, which are usually easier to determine. These are on one hand the normal invariants which form generalized cohomology groups, and hence one can use standard tools of algebraic topology to calculate them at least in principle. On the other hand there are the L-groups which are defined algebraically in terms of quadratic forms or in terms of chain complexes with quadratic structure. A great deal is known about these groups. Another part of the sequence are the surgery obstruction maps from normal invariants to the L-groups. For these maps there are certain characteristic classes formulas, which enable to calculate them in some cases. Knowledge of these three components, that means: the normal maps, the L-groups and the surgery obstruction maps is enough to determine the structure set (at least up to extension problems).
In practice one has to proceed case by case, for each manifold 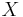 it is a unique task to determine the surgery exact sequence, see some examples below. Also note that there are versions of the surgery exact sequence depending on the category of manifolds we work with: smooth (DIFF), PL, or topological manifolds and whether we take Whitehead torsion into account or not (decorations
it is a unique task to determine the surgery exact sequence, see some examples below. Also note that there are versions of the surgery exact sequence depending on the category of manifolds we work with: smooth (DIFF), PL, or topological manifolds and whether we take Whitehead torsion into account or not (decorations  or
or  ).
).
The original 1962 work of Browder and Novikov on the existence and uniqueness of manifolds within a simply-connected homotopy type was reformulated by Sullivan in 1966 as a surgery exact sequence. In 1970 Wall developed non-simply-connected surgery theory and the surgery exact sequence for manifolds with arbitrary fundamental group.
Contents |
Definition
The surgery exact sequence is defined as
where:
the entries 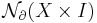 and
and 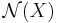 are the abelian groups of normal invariants,
are the abelian groups of normal invariants,
the entries 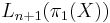 and
and 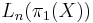 are the L-groups associated to the group ring
are the L-groups associated to the group ring ![\mathbb{Z}[\pi_1 (X)]](/2012-wikipedia_en_all_nopic_01_2012/I/de1c895c0e12ede133b29943f8abe2ee.png) ,
,
the maps 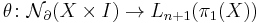 and
and 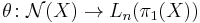 are the surgery obstruction maps,
are the surgery obstruction maps,
the arrows 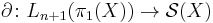 and
and 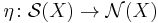 will be explained below.
will be explained below.
Versions
There are various versions of the surgery exact sequence. One can work in either of the three categories of manifolds: differentiable (smooth), PL, topological. Another possibility is to work with the decorations  or
or  .
.
The entries
Normal invariants
A degree one normal map 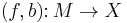 consists of the following data: an
consists of the following data: an  -dimensional oriented closed manifold
-dimensional oriented closed manifold  , a map
, a map  which is of degree one (that means
which is of degree one (that means ![f_* ([M]) = [X]](/2012-wikipedia_en_all_nopic_01_2012/I/b047b78d86a7830e61c598678d3efea5.png) , and a bundle map
, and a bundle map 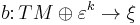 from the stable tangent bundle of
from the stable tangent bundle of  to some bundle
to some bundle 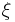 over
over  . Two such maps are equivalent if there exists a normal bordism between them (that means a bordism of the sources covered by suitable bundle data). The equivalence classes of degree one normal maps are called normal invariants.
. Two such maps are equivalent if there exists a normal bordism between them (that means a bordism of the sources covered by suitable bundle data). The equivalence classes of degree one normal maps are called normal invariants.
When defined like this the normal invariants 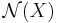 are just a pointed set, with the base point given by
are just a pointed set, with the base point given by 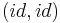 . However the Pontrjagin-Thom construction gives
. However the Pontrjagin-Thom construction gives 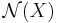 a structure of an abelian group. In fact we have a non-natural bijection
a structure of an abelian group. In fact we have a non-natural bijection
where 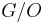 denotes the homotopy fiber of the map
denotes the homotopy fiber of the map 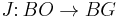 , which is an infinite loop space and hence maps into it define a generalized cohomology theory. There are corresponding identifications of the normal invariants with
, which is an infinite loop space and hence maps into it define a generalized cohomology theory. There are corresponding identifications of the normal invariants with ![[X,G/PL]](/2012-wikipedia_en_all_nopic_01_2012/I/4c0275b77b1164f13b463457d127cf00.png) when working with PL-manifolds and with
when working with PL-manifolds and with ![[X,G/TOP]](/2012-wikipedia_en_all_nopic_01_2012/I/963a8f6aae029c3c8bcbf17b814b5bea.png) when working with topological manifolds.
when working with topological manifolds.
L-groups
The  -groups are defined algebraically in terms of quadratic forms or in terms of chain complexes with quadratic structure. See the main article for more details. Here only the properties of the L-groups described below will be important.
-groups are defined algebraically in terms of quadratic forms or in terms of chain complexes with quadratic structure. See the main article for more details. Here only the properties of the L-groups described below will be important.
Surgery obstruction maps
The map 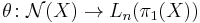 is in the first instance a set-theoretic map (that means not necessarily a homomorphism) with the following property (when
is in the first instance a set-theoretic map (that means not necessarily a homomorphism) with the following property (when 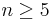 :
:
A degree one normal map 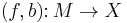 is normally cobordant to a homotopy equivalence if and only if the image
is normally cobordant to a homotopy equivalence if and only if the image 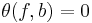 in
in ![L_n (\mathbb{Z} [\pi_1 (X)])](/2012-wikipedia_en_all_nopic_01_2012/I/19d12e180ac30aed6f70050eefc259e7.png) .
.
The normal invariants arrow 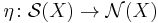
Any homotopy equivalence  defines a degree one normal map.
defines a degree one normal map.
The surgery obstruction arrow 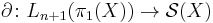
This arrow describes in fact an action of the group 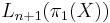 on the set
on the set 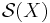 rather than just a map. The definition is based on the realization theorem for the elements of the
rather than just a map. The definition is based on the realization theorem for the elements of the  -groups which reads as follows:
-groups which reads as follows:
Let  be an
be an  -dimensional manifold with
-dimensional manifold with 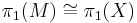 and let
and let 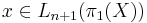 . Then there exists a degree one normal map of manifolds with boundary
. Then there exists a degree one normal map of manifolds with boundary
with the following properties:
1. 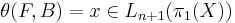
2. 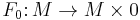 is a diffeomorphism
is a diffeomorphism
3. 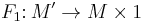 is a homotopy equivalence of closed manifolds
is a homotopy equivalence of closed manifolds
Let  represent an element in
represent an element in 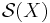 and let
and let 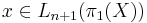 . Then
. Then 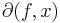 is defined as
is defined as 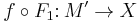 .
.
The exactness
Recall that the surgery structure set is only a pointed set and that the surgery obstruction map  might not be a homomorphism. Hence it is necessary to explain what is meant when talking about the "exact sequence". So the surgery exact sequence is an exact sequence in the following sense:
might not be a homomorphism. Hence it is necessary to explain what is meant when talking about the "exact sequence". So the surgery exact sequence is an exact sequence in the following sense:
For a normal invariant 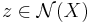 we have
we have  if and only if
if and only if 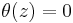 . For two manifold structures
. For two manifold structures 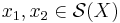 we have
we have  if and only if there exists
if and only if there exists 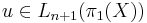 such that
such that 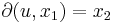 . For an element
. For an element 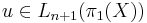 we have
we have 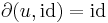 if and only if
if and only if 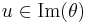 .
.
Versions revisited
In the topological category the surgery obstruction map can be made into a homomorphism. This is achieved by putting an alternative abelian group structure on the normal invariants as described here. Moreover, the surgery exact sequence can be identified with the algebraic surgery exact sequence of Ranicki which is an exact sequence of abelian groups by definition. This gives the structure set 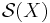 the structure of an abelian group. Note, however, that there is to this date no satisfactory geometric description of this abelian group structure.
the structure of an abelian group. Note, however, that there is to this date no satisfactory geometric description of this abelian group structure.
Classification of manifolds
The answer to the organizing questions of the surgery theory can be formulated in terms of the surgery exact sequence. In both cases the answer is given in the form of a two-stage obstruction theory.
The existence question. Let  be a finite Poincaré complex. It is homotopy equivalent to a manifold if and only if the following two conditions are satisfied. Firstly,
be a finite Poincaré complex. It is homotopy equivalent to a manifold if and only if the following two conditions are satisfied. Firstly,  must have a vector bundle reduction of its Spivak normal fibration. This condition can be also formulated as saying that the set of normal invariants
must have a vector bundle reduction of its Spivak normal fibration. This condition can be also formulated as saying that the set of normal invariants 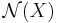 is non-empty. Secondly, there must be a normal invariant
is non-empty. Secondly, there must be a normal invariant 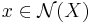 such that
such that 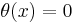 . Equivalently, the surgery obstruction map
. Equivalently, the surgery obstruction map 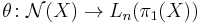 hits
hits 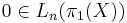 .
.
The uniqueness question. Let  and
and 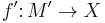 represent two elements in the surgery structure set
represent two elements in the surgery structure set 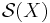 . The question whether they represent the same element can be answered in two stages as follows. First there must be a normal cobordism between the degree one normal maps induced by
. The question whether they represent the same element can be answered in two stages as follows. First there must be a normal cobordism between the degree one normal maps induced by 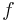 and
and 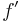 , this means
, this means  in
in 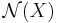 . Denote the normal cobordism
. Denote the normal cobordism 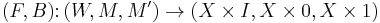 . If the surgery obstruction
. If the surgery obstruction 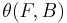 in
in 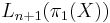 to make this normal cobordism to an h-cobordism (or s-cobordism) relative to the boundary vanishes then
to make this normal cobordism to an h-cobordism (or s-cobordism) relative to the boundary vanishes then 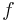 and
and 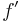 in fact represent the same element in the surgery structure set.
in fact represent the same element in the surgery structure set.
Examples
1. Homotopy spheres
This is an example in the smooth category, 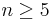 .
.
The idea of the surgery exact sequence is implicitly present already in the original article of Kervaire and Milnor on the groups of homotopy spheres. In the present terminology we have
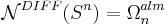 the cobordism group of almost framed
the cobordism group of almost framed  manifolds,
manifolds, 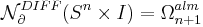
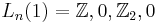 where
where 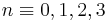 mod
mod 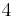 (recall the
(recall the 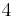 -periodicity of the L-groups)
-periodicity of the L-groups)
The surgery exact sequence in this case is an exact sequence of abelian groups. In addition to the above identifications we have
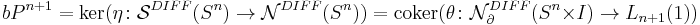
Because the odd-dimensional L-groups are trivial one obtains these exact sequences:
The results of Kervaire and Milnor are obtained by studying the middle map in the first two sequences and by relating the groups 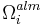 to stable homotopy theory.
to stable homotopy theory.
2. Topological spheres
The generalized Poincaré conjecture in dimension  can be phrased as saying that
can be phrased as saying that 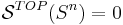 . It has been proved for any
. It has been proved for any  by the work of Smale, Freedman and Perelman. From the surgery exact sequence for
by the work of Smale, Freedman and Perelman. From the surgery exact sequence for 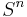 for
for 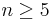 in the topological category we see that
in the topological category we see that
is an isomorphism. (In fact this can be extended to 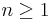 by some ad-hoc methods.)
by some ad-hoc methods.)
3. Complex projective spaces in the topological category
The complex projective space 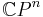 is a
is a 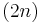 -dimensional topological manifold with
-dimensional topological manifold with 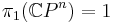 . In addition it is known that in the case
. In addition it is known that in the case 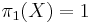 in the topological category the surgery obstruction map
in the topological category the surgery obstruction map  is always surjective. Hence we have
is always surjective. Hence we have
From the work of Sullivan one can calculate
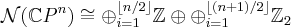 and hence
and hence 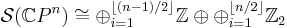
4. Aspherical manifolds in the topological category
An aspherical  -dimensional manifold
-dimensional manifold  is an
is an  -manifold such that
-manifold such that 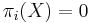 for
for 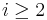 . Hence the only non-trivial homotopy group is
. Hence the only non-trivial homotopy group is 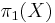
One way to state the Borel conjecture is to say that for such  we have that the Whitehead group
we have that the Whitehead group 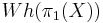 is trivial and that
is trivial and that
This conjecture was proven in many special cases - for example when 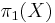 is
is 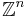 , when it is the fundamental group of a negatively curved manifold or when it is a word-hyperbolic group or a CAT(0)-group.
, when it is the fundamental group of a negatively curved manifold or when it is a word-hyperbolic group or a CAT(0)-group.
The statement is equivalent to showing that the surgery obstruction map to the right of the surgery structure set is injective and the surgery obstruction map to the left of the surgery structure set is surjective. Most of the proofs of the above mentioned results are done by studying these maps or by studying the assembly maps with which they can be identified. See more details in Borel conjecture, Farrell-Jones Conjecture.
References
- Browder, William (1972), Surgery on simply-connected manifolds, Berlin, New York: Springer-Verlag, MR0358813
- Lück, Wolfgang (2002), A basic introduction to surgery theory, ICTP Lecture Notes Series 9, Band 1, of the school "High-dimensional manifold theory" in Trieste, May/June 2001, Abdus Salam International Centre for Theoretical Physics, Trieste 1-224, http://wwwmath.uni-muenster.de/reine/inst/lueck/homepages/wolfgang_lueck/data/ictp.pdf
- Ranicki, Andrew (1992), Algebraic L-theory and topological manifolds, Cambridge Tracts in Mathematics, 102, Cambridge University Press, http://www.maths.ed.ac.uk/~aar/books/topman.pdf
- Ranicki, Andrew (2002), Algebraic and Geometric Surgery, Oxford Mathematical Monographs, Clarendon Press, ISBN 978-0-19-850924-0, MR2061749, http://www.maths.ed.ac.uk/~aar/books/surgery.pdf
- Wall, C. T. C. (1999), Surgery on compact manifolds, Mathematical Surveys and Monographs, 69 (2nd ed.), Providence, R.I.: American Mathematical Society, ISBN 978-0-8218-0942-6, MR1687388
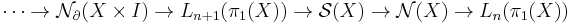
![\mathcal{N} (X) \cong [X,G/O]](/2012-wikipedia_en_all_nopic_01_2012/I/d72de15e3da91e9e1ac4e6f21c5ca9f4.png)