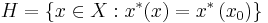Supporting hyperplane
Supporting hyperplane is a concept in geometry. A hyperplane divides a space into two half-spaces. A hyperplane is said to support a set  in Euclidean space
in Euclidean space 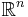 if it meets both of the following:
if it meets both of the following:
 is entirely contained in one of the two closed half-spaces determined by the hyperplane
is entirely contained in one of the two closed half-spaces determined by the hyperplane has at least one point on the hyperplane.
has at least one point on the hyperplane.
Here, a closed half-space is the half-space that includes the hyperplane.
Supporting hyperplane theorem
This theorem states that if  is a closed convex set in a topological vector space
is a closed convex set in a topological vector space 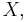 and
and 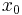 is a point on the boundary of
is a point on the boundary of 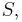 then there exists a supporting hyperplane containing
then there exists a supporting hyperplane containing 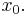 If
If 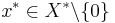 (the dual space of X) such that
(the dual space of X) such that 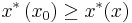 for all
for all 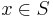 , then
, then
defines a supporting hyperplane.[1]
Conversely, if  is a closed set with nonempty interior such that every point has a supporting hyperplane, then
is a closed set with nonempty interior such that every point has a supporting hyperplane, then  is a convex set.[1]
is a convex set.[1]
The hyperplane in the theorem may not be unique, as noticed in the second picture on the right. If the closed set  is not convex, the statement of the theorem is not true at all points on the boundary of
is not convex, the statement of the theorem is not true at all points on the boundary of 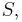 as illustrated in the third picture on the right.
as illustrated in the third picture on the right.
A related result is the separating hyperplane theorem.
See also
References
- ^ a b Boyd, Stephen P.; Vandenberghe, Lieven (2004) (pdf). Convex Optimization. Cambridge University Press. pp. 50–51. ISBN 9780521833783. http://www.stanford.edu/~boyd/cvxbook/bv_cvxbook.pdf. Retrieved October 15, 2011.
- Ostaszewski, Adam (1990). Advanced mathematical methods. Cambridge; New York: Cambridge University Press. p. 129. ISBN 0521289645.
- Giaquinta, Mariano; Hildebrandt, Stefan (1996). Calculus of variations. Berlin; New York: Springer. p. 57. ISBN 354050625X.
- Goh, C. J.; Yang, X.Q. (2002). Duality in optimization and variational inequalities. London; New York: Taylor & Francis. p. 13. ISBN 0415274796.