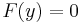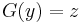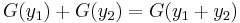Superposition principle
In physics and systems theory, the superposition principle [1], also known as superposition property, states that, for all linear systems, the net response at a given place and time caused by two or more stimuli is the sum of the responses which would have been caused by each stimulus individually. So that if input A produces response X and input B produces response Y then input (A + B) produces response (X + Y).
Mathematically, for a linear system, F, defined by F(x) = y, where x is some sort of stimulus (input) and y is some sort of response (output), the superposition (i.e., sum) of stimuli yields a superposition of the respective responses:
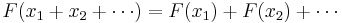 .
.
The superposition principle holds because, by definition, a linear system must be additive. Superposition may sometimes imply linearity, depending on whether homogeneity is included or implied in the definition of superposition.
In the field of electrical engineering, where the x and y signals are allowed to be complex-valued (as is common in signal processing), a linear system must satisfy the superposition property, which requires the system to be additive and homogeneous.[2][3] An additive system satisfies 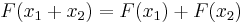 . A homogeneous system satisfies
. A homogeneous system satisfies  , where a is a scalar. Often the additivity and homogeneity conditions for superposition are combined into a single condition, defined as
, where a is a scalar. Often the additivity and homogeneity conditions for superposition are combined into a single condition, defined as
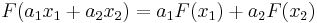 ,
,
This principle has many applications in physics and engineering because many physical systems can be modeled as linear systems. For example, a beam can be modeled as a linear system where the input stimulus is the load on the beam and the output response is the deflection of the beam. Because physical systems are generally only approximately linear, the superposition principle is only an approximation of the true physical behavior; it provides insight for typical operational regions for these systems.
The superposition principle applies to any linear system, including algebraic equations, linear differential equations, and systems of equations of those forms. The stimuli and responses could be numbers, functions, vectors, vector fields, time-varying signals, or any other object which satisfies certain axioms. Note that when vectors or vector fields are involved, a superposition is interpreted as a vector sum.
Contents |
Relation to Fourier analysis and similar methods
By writing a very general stimulus (in a linear system) as the superposition of stimuli of a specific, simple form, often the response becomes easier to compute,
For example, in Fourier analysis, the stimulus is written as the superposition of infinitely many sinusoids. Due to the superposition principle, each of these sinusoids can be analyzed separately, and its individual response can be computed. (The response is itself a sinusoid, with the same frequency as the stimulus, but generally a different amplitude and phase.) According to the superposition principle, the response to the original stimulus is the sum (or integral) of all the individual sinusoidal responses.
As another common example, in Green's function analysis, the stimulus is written as the superposition of infinitely many impulse functions, and the response is then a superposition of impulse responses.
Fourier analysis is particularly common for waves. For example, in electromagnetic theory, ordinary light is described as a superposition of plane waves (waves of fixed frequency, polarization, and direction). As long as the superposition principle holds (which is often but not always; see nonlinear optics), the behavior of any light wave can be understood as a superposition of the behavior of these simpler plane waves.
Application to waves
Waves are usually described by variations in some parameter through space and time—for example, height in a water wave, pressure in a sound wave, or the electromagnetic field in a light wave. The value of this parameter is called the amplitude of the wave, and the wave itself is a function specifying the amplitude at each point.
In any system with waves, the waveform at a given time is a function of the sources (i.e., external forces, if any, that create or affect the wave) and initial conditions of the system. In many cases (for example, in the classic wave equation), the equation describing the wave is linear. When this is true, the superposition principle can be applied. That means that the net amplitude caused by two or more waves traversing the same space, is the sum of the amplitudes which would have been produced by the individual waves separately. For example, two waves traveling towards each other will pass right through each other without any distortion on the other side. (See image at top.)
Wave interference
The phenomenon of interference between waves is based on this idea. When two or more waves traverse the same space, the net amplitude at each point is the sum of the amplitudes of the individual waves. In some cases, such as in noise-cancelling headphones, the summed variation has a smaller amplitude than the component variations; this is called destructive interference. In other cases, such as in Line Array, the summed variation will have a bigger amplitude than any of the components individually; this is called constructive interference.
| combined waveform |
||
| wave 1 | ||
| wave 2 | ||
| Two waves in phase | Two waves 180° out of phase |
|
Departures from linearity
In most realistic physical situations, the equation governing the wave is only approximately linear. In these situations, the superposition principle only approximately holds. As a rule, the accuracy of the approximation tends to improve as the amplitude of the wave gets smaller. For examples of phenomena that arise when the superposition principle does not exactly hold, see the articles nonlinear optics and nonlinear acoustics.
Quantum superposition
In quantum mechanics, a principal task is to compute how a certain type of wave propagates and behaves. The wave is called a wavefunction, and the equation governing the behavior of the wave is called Schrödinger's wave equation. A primary approach to computing the behavior of a wavefunction is to write that wavefunction as a superposition (called "quantum superposition") of (possibly infinitely many) other wavefunctions of a certain type—stationary states whose behavior is particularly simple. Since Schrödinger's wave equation is linear, the behavior of the original wavefunction can be computed through the superposition principle this way.[4] See Quantum superposition.
Boundary value problems
A common type of boundary value problem is (to put it abstractly) finding a function y that satisfies some equation
with some boundary specification
For example, in Laplace's equation with Dirichlet boundary conditions, F would be the Laplacian operator in a region R, G would be an operator that restricts y to the boundary of R, and z would be the function that y is required to equal on the boundary of R.
In the case that F and G are both linear operators, then the superposition principle says that a superposition of solutions to the first equation is another solution to the first equation:
- IF
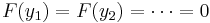 THEN
THEN 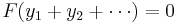
while the boundary values superpose:
Using these facts, if a list can be compiled of solutions to the first equation, then these solutions can be carefully put into a superposition such that it will satisfy the second equation. This is one common method of approaching boundary value problems.
Other example applications
- In electrical engineering, in a linear circuit, the input (an applied time-varying voltage signal) is related to the output (a current or voltage anywhere in the circuit) by a linear transformation. Thus, a superposition (i.e., sum) of input signals will yield the superposition of the responses. The use of Fourier analysis on this basis is particularly common. For another, related technique in circuit analysis, see Superposition theorem.
- In physics, Maxwell's equations imply that the (possibly time-varying) distributions of charges and currents are related to the electric and magnetic fields by a linear transformation. Thus, the superposition principle can be used to simplify the computation of fields which arise from given charge and current distribution. The principle also applies to other linear differential equations arising in physics, such as the heat equation.
- In mechanical engineering, superposition is used to solve for beam and structure deflections of combined loads when the effects are linear (i.e., each load does not affect the results of the other loads, and the effect of each load does not significantly alter the geometry of the structural system).[5]
- In hydrogeology, the superposition principle is applied to the drawdown of two or more water wells pumping in an ideal aquifer.
- In process control, the superposition principle is used in model predictive control.
- The superposition principle can be applied when small deviations from a known solution to a nonlinear system are analyzed by linearization.
- In music, theorist Joseph Schillinger used a form of the superposition principle as one basis of his Theory of Rhythm in his Schillinger System of Musical Composition.
See also
- Impulse response
- Green's function
- Quantum superposition
- Interference
- Coherence (physics)
- Convolution
References
- ^ The Penguin Dictionary of Physics, ed. Valerie Illingworth, 1991, Penguin Books, London
- ^ a b Oppenheim, A. V., Willsky, A. S., & Nawab, S. H. Signals & Systems. Prentice Hall. 1997.
- ^ a b Hsu, Hwei P. Signals and Systems. McGraw-Hill. 1995. p.18. ISBN 0-07-030641-9
- ^ Quantum Mechanics, Kramers, H.A. publisher Dover, 1957, p. 62 ISBN 978-0486667720
- ^ Mechanical Engineering Design, By Joseph Edward Shigley, Charles R. Mischke, Richard Gordon Budynas, Published 2004 McGraw-Hill Professional, p. 192 ISBN 0072520361
Further reading
- Haberman, Richard (2004). Applied Partial Differential Equations. Prentice Hall. ISBN 0-13-065243-1.
- Superposition of sound waves