Superpattern

In mathematics (and specifically in combinatorics), k-superpattern is a permutation of minimal length that contains all permutation patterns of length k.

Examples

Consider the permutation 25314, which has length 5. It has 10 subsequences of length 3, including 253, 251, 234, 531, 534 and 314. (That is, we take 3 entries at a time, keeping the order preserved.) In each subsequence, we replace the smallest entry with 1, the next largest entry with 2, and the largest with 3. Thus, 253 gets renumbered to 132, 251 to 231, and so on. (If we had chosen subsequences of longer length, we would replace the third-smallest with 3, the fourth-smallest with 4, etc. That is, we apply an order-isomorphism to each subsequence to get a permutation.)

Applying this operation to the six selected subsequences gives 132, 231, 123, 321, 312 and 213. In fact, this list contains all the possible 3-subpatterns, that is, all 6 (3 factorial) permutations of length 3. From this, we can see that 25314 contains all possible 3-subpatterns. This is one of the two conditions to be a 3-superpattern. The other condition is that there should be no shorter permutation with the same property.

Consider also that in order to have 123 and 321 as subpatterns in the same permutation, by the inclusion-exclusion principle we need a minimum of 3 + 3 - 1 = 5 numbers (since only one number can be in both the largest increasing sequence and the largest decreasing sequence). This implies that any permutation which contains both 123 and 321 as subpatterns must be at least 5 digits long. Since 25314 has length 5 it is therefore a 3-superpattern of length 5.

Bounds on the length of superpatterns

Let 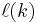$\ell(k)$ denote the length of k-superpatterns.

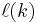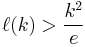The only known lower bound for $\ell(k)$ is $\ell(k) > \frac{k^2}{e}$ . This bound follows from the observation that if a permutation of length n contains all permutations of length k as patterns then 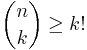$\binom{n}{k} \ge k!$ . Applying standard estimates for binomial coefficients and factorials (e.g., related to Stirling's approximation) yields the result.

The upper bound 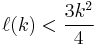$\ell(k) < \frac{3k^2}{4}$ can be shown by probabilistic means.

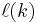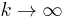It is believed that $\ell(k)$ approaches k²/2 in the limit as $k \to \infty$ .

References

Bóna, Miklós (2002). A walk through combinatorics: an introduction to enumeration and graph theory. London: World Scientific. ISBN 9810249012.
Packing patterns into words