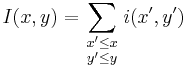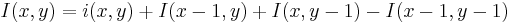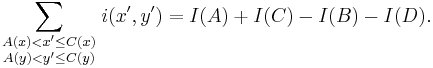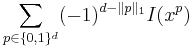Summed area table
A summed area table (also known as an integral image) is an algorithm for quickly and efficiently generating the sum of values in a rectangular subset of a grid. It was first introduced to the computer graphics world in 1984 for use in mipmaps but wasn't widely used in the computer vision community until its prominent use in the Viola–Jones object detection framework twenty years later.
Contents |
The algorithm
As the name suggests, the value at any point (x, y) in the summed area table is just the sum of all the pixels above and to the left of (x, y), inclusive:[1][2]
Moreover, the summed area table can be computed efficiently in a single pass over the image, using the fact that the value in the summed area table at (x, y) is just:
Once the summed area table has been computed, the task of evaluating any rectangle can be accomplished in constant time with just four array references. Specifically, using the notation in the figure at right, the value is just
Extensions
This method is naturally extended to continuous domains [3].
The method can be also extended to high dimensional images[4]. If the corners of the rectangle are 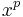 with
with  in
in 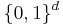 , then the sum of image values contained in the rectagle are computed with the formula
, then the sum of image values contained in the rectagle are computed with the formula
where 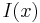 is the integral image at
is the integral image at  and
and  the image dimension. The notation
the image dimension. The notation 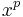 correspond in the example to
correspond in the example to 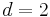 ,
, 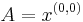 ,
, 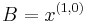 ,
, 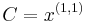 and
and 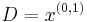 . In neuroimaging, for example, the images have dimension
. In neuroimaging, for example, the images have dimension 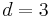 or
or 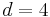 , when using voxels or voxels with time-stamp.
, when using voxels or voxels with time-stamp.
Video Lectures
- An introduction to the theory behind the integral image algorithm
- A demonstration to a continuous version of the integral image algorithm, from the Wolfram Demonstrations Project
References
- ^ Crow, Franklin (1984). "Summed-area tables for texture mapping". SIGGRAPH '84: Proceedings of the 11th annual conference on Computer graphics and interactive techniques. pp. 207–212. http://www.soe.ucsc.edu/classes/cmps160/Fall05/papers/p207-crow.pdf.
- ^ Viola, Paul; Jones, Michael (2002). "Robust Real-time Object Detection". International Journal of Computer Vision. http://research.microsoft.com/~viola/Pubs/Detect/violaJones_IJCV.pdf.
- ^ Finkelstein, Amir (2010). "Double Integrals By Summing Values Of Cumulative Distribution Function". Wolfram Demonstration Project. http://demonstrations.wolfram.com/DoubleIntegralsBySummingValuesOfACumulativeDistributionFunct/.
- ^ Tapia, Ernesto (January 2011). "A note on the computation of high-dimensional integral images". Pattern Recognition Letters 32 (2). doi:10.1016/j.patrec.2010.10.007.