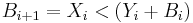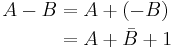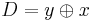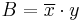Subtractor
In electronics, a subtractor can be designed using the same approach as that of an adder. The binary subtraction process is summarized below. As with an adder, in the general case of calculations on multi-bit numbers, three bits are involved in performing the subtraction for each bit of the difference: the minuend (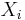 ), subtrahend (
), subtrahend (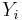 ), and a borrow in from the previous (less significant) bit order position (
), and a borrow in from the previous (less significant) bit order position (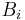 ). The outputs are the difference bit (
). The outputs are the difference bit (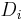 ) and borrow bit
) and borrow bit 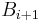 . The subtractor is best understood by considering that the substrahend and both borrow bits have negative weights, whereas the X and D bits are positive. The operation performed by the subtractor is to rewrite
. The subtractor is best understood by considering that the substrahend and both borrow bits have negative weights, whereas the X and D bits are positive. The operation performed by the subtractor is to rewrite 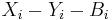 (which can take the values -2, -1, 0, or 1) as the sum
(which can take the values -2, -1, 0, or 1) as the sum 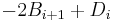 .
.
Subtractors are usually implemented within a binary adder for only a small cost when using the standard two's complement notation, by providing an addition/subtraction selector to the carry-in and to invert the second operand.
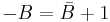 (definition of two's complement negation)
(definition of two's complement negation)
Contents |
Half subtractor
The half-subtractor is a combinational circuit which is used to perform subtraction of two bits. It has two inputs, X (minuend) and Y (subtrahend) and two outputs D (difference) and B (borrow).
Truth table
The truth table for the half subtractor is given below.[1]
| X | Y | D | B |
|---|---|---|---|
| 0 | 0 | 0 | 0 |
| 0 | 1 | 1 | 1 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 0 |
From the above table one can draw the Karnaugh map for "difference" and "borrow".
So, Logic equations are:
Full subtractor
The full-subtractor is a combinational circuit which is used to perform subtraction of three bits. It has three inputs, X (minuend) and Y (subtrahend) and Z (subtrahend) and two outputs D (difference) and B (borrow).
D=X-Y-Z (don't bother about sign)
B = 1 If X<(Y+Z)
Truth table
The truth table for the full subtractor is given below.[1]
| x | y | z | D | B |
|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 1 | 1 |
| 0 | 1 | 0 | 1 | 1 |
| 0 | 1 | 1 | 0 | 1 |
| 1 | 0 | 0 | 1 | 0 |
| 1 | 0 | 1 | 0 | 0 |
| 1 | 1 | 0 | 0 | 0 |
| 1 | 1 | 1 | 1 | 1 |
So, Logic equations are: