Submodular set function
In mathematics, submodular functions are set functions which usually appear in approximation algorithms, functions modeling user preferences in game theory. These functions have a natural diminishing returns property which makes them suitable for many applications.
Contents |
Definition
Submodular function is a set function 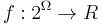 which satisfies one of the following equivalent definitions[1].
which satisfies one of the following equivalent definitions[1].
- For every
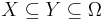 and
and 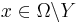 we have that
we have that 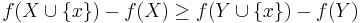
- For every
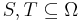 we have that
we have that 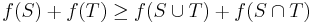
- For every
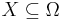 and
and 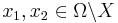 we have that
we have that 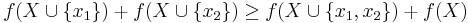
A submodular function is also a subadditive function, but a subadditive function need not be submodular.
Applications
Types
Monotone Submodular function
A submodular function  is said to be monotone if for every
is said to be monotone if for every 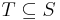 we have that
we have that 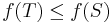 .
.
- Examples of Monotone Submodular function
- Linear functions
- Any function of the form
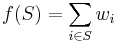 is called a linear function. Additionally if
is called a linear function. Additionally if 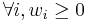 then f is montone.
then f is montone.
- Any function of the form
- Budget-additive functions
- Any function of the form
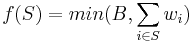 for each
for each 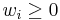 and
and 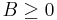 is called budget additive.
is called budget additive.
- Any function of the form
- Coverage function
- Let
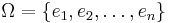 be the ground set. Consider a universe
be the ground set. Consider a universe  and a set of sets
and a set of sets 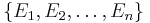 of the universe
of the universe  . Then a coverage function is defined for any set
. Then a coverage function is defined for any set 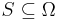 as
as  .
.
- Let
- Entropy
- Let
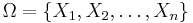 be a set of random variables. Then for any
be a set of random variables. Then for any 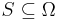 we have that
we have that 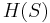 is a submodular function, where
is a submodular function, where 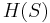 is the entropy of the set of random variables
is the entropy of the set of random variables 
- Let
- Matroid rank functions
- Let
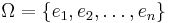 be the ground set on which a matroid is defined. Then the rank function of the matroid is a submodular function.
be the ground set on which a matroid is defined. Then the rank function of the matroid is a submodular function.
- Let
Non-monotone Submodular function
A submodular function  which is not necessarily monotone is called as Non-monotone Submodular function.
which is not necessarily monotone is called as Non-monotone Submodular function.
Symmetric Non-monotone Submodular function
A submodular function  is called symmetric if for every
is called symmetric if for every 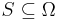 we have that
we have that 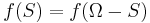
- Examples of Symmetric Non-Monotone Submodular function
- Graph cuts
- Let
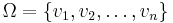 be the vertices of a graph. For any set of vertices
be the vertices of a graph. For any set of vertices 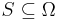 let
let 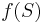 denote the number of edges
denote the number of edges 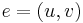 such that
such that 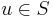 and
and 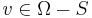 .
.
- Let
- Mutual information
- Let
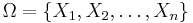 be a set of random variables. Then for any
be a set of random variables. Then for any 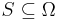 we have that
we have that 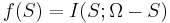 is a submodular function, where
is a submodular function, where 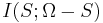 is the mutual information.
is the mutual information.
- Let
Asymmetric Non-monotone Submodular function
A submodular function  is called Asymmetric if it is not necessarily symmetric.
is called Asymmetric if it is not necessarily symmetric.
- Examples of Symmetric Non-Monotone Submodular function
- Directed graph cuts
- Let
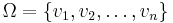 be the vertices of a directed graph. For any set of vertices
be the vertices of a directed graph. For any set of vertices 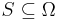 let
let 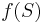 denote the number of edges
denote the number of edges 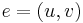 such that
such that 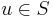 and
and 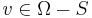 .
.
- Let
Continuous extensions
Lovasz extension
Consider any vector 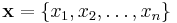 such that each
such that each 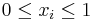 . Then the lovasz extension is defined as
. Then the lovasz extension is defined as 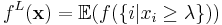 where the expectation is over choosing
where the expectation is over choosing  uniformly in
uniformly in ![[0,1]](/2012-wikipedia_en_all_nopic_01_2012/I/ccfcd347d0bf65dc77afe01a3306a96b.png) . It can be shown that Lovasz extension is a convex function.
. It can be shown that Lovasz extension is a convex function.
Multilinear extension
Consider any vector 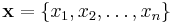 such that each
such that each 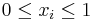 . Then the multilinear extension is defined as
. Then the multilinear extension is defined as 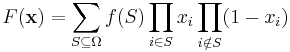
Convex Closure
Consider any vector 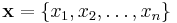 such that each
such that each 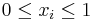 . Then the convex closure is defined as
. Then the convex closure is defined as 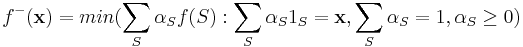 . It can be shown that
. It can be shown that 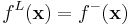
Concave Closure
Consider any vector 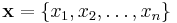 such that each
such that each 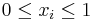 . Then the convex closure is defined as
. Then the convex closure is defined as 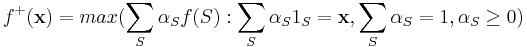 .
.
Properties
Operations which preserve Submodularity
- Non-negative linear combinations. Consider any submodular function
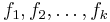 and non negative numbers
and non negative numbers 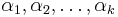 . Then
. Then 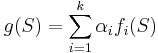 is a submodular function.
is a submodular function. - Consider any monotone submodular function
 and a non negative number
and a non negative number  . Then
. Then 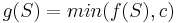 is also a submodular function.
is also a submodular function. - Consider any submodular function
 . Then
. Then 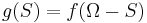 is also a submodular function.
is also a submodular function.
Optimization problems
Submodular functions have properties which are very similar to convex and concave functions. Hence a lot of optimization problems can be cast as maximizing or minimizing submodular functions subject to various constraints.
- Minimization of submodular functions.
- Under the simplest case the problem is to find set
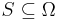 which minimizes submodular function subject to no constraints. A series of results [2][3][4][5] have established the polynomial time solvability of this problem. Finding minimum cut in a graph is a special case of this problem.
which minimizes submodular function subject to no constraints. A series of results [2][3][4][5] have established the polynomial time solvability of this problem. Finding minimum cut in a graph is a special case of this problem.
- Under the simplest case the problem is to find set
- Maximization of submodular functions.
- Unlike minimization, maximization of submodular functions is typically NP-hard. A host of problems such as max cut, maximum coverage problem can be cast as special cases of this problem under suitable constraints. Typically the approximation algorithms for these problems are based on either greedy or local search type of algorithms.
- Maximizing a Symmetric Non-montone Submodular function subject to no constraint. This problem admits a 1/2 approximation algorithm[6]. Finding max cut is a special case of this problem.
- Maximizing a Montone Submodular function subject to cardinality constraint. This problem admits a 1-1/e approximation algorithm[7]. Maximum coverage problem is a special case of this problem.
See also
Citations
- ^ (Schrijver 2003, §44, p. 766)
- ^ M. Grotschel, L. Lovasz, and A. Schrijver , The ellipsoid method and its consequences in combinatorial optimization,Combinatorica,1 (1981),pp. 169–197.
- ^ W. H. Cunningham, On submodular function minimization, Combinatorica,5 (1985),pp. 185–192.
- ^ S. Iwata, L. Fleischer, and S. Fujishige, A combinatorial strongly polynomial algorithm for minimizing submodular functions,J. ACM,48 (2001),pp. 761–777
- ^ A. Schrijver, A combinatorial algorithm minimizing submodular functions in strongly polynomial time,J. Combin. Theory Ser. B,80 (2000),pp. 346–355.
- ^ U. Feige, V. Mirrokni and J. Vondr´ak. Maximizing non-monotone submodular functions, Proc. of 48th FOCS (2007), 461–471.
- ^ G. L. Nemhauser, L. A. Wolsey and M. L. Fisher. An analysis of approximations for maximizing submodular set functions I, Mathematical Programming 14 (1978), 265–294
References
General References
- Schrijver, Alexander (2003), Combinatorial Optimization, Springer, ISBN 3540443894
- Lee, Jon (2004), A First Course in Combinatorial Optimization, Cambridge University Press, ISBN 0521010128
- Fujishige, Saruto (2005), Submodular Functions and Optimization, Elsevier, ISBN 0444520864
- Narayanan, H. (1997), Submodular Functions and Electrical Networks, ISBN 0444825231