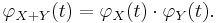Subindependence

In probability theory and statistics, subindependence is a weak form of independence.

Two random variables X and Y are said to be subindependent if the characteristic function of their sum is equal to the product of their marginal characteristic functions. Symbolically:

This is a generalization of the concept of independence of random variables, i.e. if two random variables are independent then they are subindependent, but not conversely. If two random variables are subindependent, and if their covariance exists, then they are uncorrelated.^[1]

Subindependence has some peculiar properties: for example, there exist random variables X and Y that are subindependent, but X and αY are not subindependent when α ≠ 1.^[1]

There is at least one example case of a joint distribution where the variables are subindependent, but not independent.^[1]

Notes

Reference

• Hamedani, G.G.; Volkmer, H.W. (2009). "Letter". The American Statistician 63 (3): 295–295. 

Further reading

• Hamedani, G.G.; Walter, G.G. (1984). "A fixed point theorem and its application to the central limit theorem". Archiv der Mathematik 43 (3): 258–264. doi:10.1007/BF01247572. http://www.springerlink.com/content/V1X06V0105MMG676. 
• Hamedani, G.G. (2003). "Why independence when all you need is sub-independence". Journal of Statistical Theory and Applications 1 (4): 280–283.