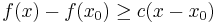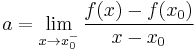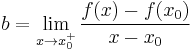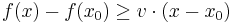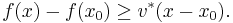Subderivative

In mathematics, the concepts of subderivative, subgradient, and subdifferential arise in convex analysis, that is, in the study of convex functions, often in connection to convex optimization.

Let f:I→R be a real-valued convex function defined on an open interval of the real line. Such a function need not be differentiable at all points: For example, the absolute value function f(x)=|x| is nondifferentiable when x=0. However, as seen in the picture on the right, for any x₀ in the domain of the function one can draw a line which goes through the point (x₀, f(x₀)) and which is everywhere either touching or below the graph of f. The slope of such a line is called a subderivative (because the line is under the graph of f).

1 Definition
2 Examples
3 Properties
4 The subgradient
5 See also
6 References

Definition

Rigorously, a subderivative of a function f:I→R at a point x₀ in the open interval I is a real number c such that

$f(x)-f(x_0)\ge c(x-x_0)$

for all x in I. One may show that the set of subderivatives at x₀ for a convex function is a nonempty closed interval [a, b], where a and b are the one-sided limits

$a=\lim_{x\to x_0^-}\frac{f(x)-f(x_0)}{x-x_0}$

$b=\lim_{x\to x_0^%2B}\frac{f(x)-f(x_0)}{x-x_0}$

which are guaranteed to exist and satisfy a ≤ b.

The set [a, b] of all subderivatives is called the subdifferential of the function f at x₀. If f is convex and its subdifferential at 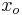$x_o$ contains exactly one subderivative, then f is differentiable at 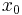$x_0$ .^[1]

Examples

Consider the function f(x)=|x| which is convex. Then, the subdifferential at the origin is the interval [−1, 1]. The subdifferential at any point x₀<0 is the singleton set {−1}, while the subdifferential at any point x₀>0 is the singleton {1}.

Properties

A convex function f:I→R is differentiable at x₀ if and only if the subdifferential is made up of only one point, which is the derivative at x₀.

A point x₀ is a global minimum of a convex function f if and only if zero is contained in the subdifferential, that is, in the figure above, one may draw a horizontal "subtangent line" to the graph of f at (x₀, f(x₀)). This last property is a generalization of the fact that the derivative of a function differentiable at a local minimum is zero.

The subgradient

The concepts of subderivative and subdifferential can be generalized to functions of several variables. If f:U→ R is a real-valued convex function defined on a convex open set in the Euclidean space Rⁿ, a vector v in that space is called a subgradient at a point x₀ in U if for any x in U one has

$f(x)-f(x_0)\ge v\cdot (x-x_0)$

where the dot denotes the dot product. The set of all subgradients at x₀ is called the subdifferential at x₀ and is denoted ∂f(x₀). The subdifferential is always a nonempty convex compact set.

These concepts generalize further to convex functions f:U→ R on a convex set in a locally convex space V. A functional v^∗ in the dual space V^∗ is called subgradient at x₀ in U if

$f(x)-f(x_0)\ge v^*(x-x_0).$

The set of all subgradients at x₀ is called the subdifferential at x₀ and is again denoted ∂f(x₀). The subdifferential is always a convex closed set. It can be an empty set; consider for example an unbounded operator, which is convex, but has no subgradient. If f is continuous, the subdifferential is nonempty.

References

^ R. T. Rockafellar Convex analysis 1970. Theorem 25.1, p.242

Jean-Baptiste Hiriart-Urruty, Claude Lemaréchal, Fundamentals of Convex Analysis, Springer, 2001. ISBN 3-540-42205-6.
Zălinescu, C.. Convex analysis in general vector spaces. World Scientific Publishing Co., Inc. pp. xx+367. ISBN 981-238-067-1. MR 1921556.